题目内容
16. 如图所示,A、B两物体的质量分别是m1和m2,其接触面光滑,与水平面的夹角为θ,若A、B与水平地面的动摩擦系数都是μ,用水平力F推A,使A、B一起加速运动,求:
如图所示,A、B两物体的质量分别是m1和m2,其接触面光滑,与水平面的夹角为θ,若A、B与水平地面的动摩擦系数都是μ,用水平力F推A,使A、B一起加速运动,求:(1)A、B间的相互作用力
(2)为维持A、B间不发生相对滑动,力F的取值范围.
(3)当A、B与水平地面间光滑时,且又m1=m2=m时,则F的取值范围是多少?
分析 (1)对A、B系统根据牛顿第二定律求加速度;隔离B,根据牛顿第二定律求出A、B间的相互作用力;
(2)(3)分别以m1和(m1+m2)组成的整体为研究的对象,对它们进行受力分析,结合牛顿第二定律列出方程,即可求解.
解答 解:(1)对A、B组成的整体,根据牛顿第二定律,有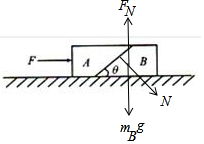
F-μ(m1+m2)g=(m1+m2)a
解得:$a=\frac{F}{{m}_{1}+{m}_{2}}$-μg
隔离B,对B受力分析如图,
根据牛顿第二定律,有
Nsinθ-μm2g=m2a
解得:N=$\frac{{m}_{2}F}{({m}_{1}+{m}_{2})sinθ}$
(2)若要二者一起做加速运动,则推力要大于摩擦力,即:F>μ(m1+m2)g
当m1恰好要相对于m2发生运动时,F达到最大值.此时m1在竖直方向上不再受到地面的支持力,它只受到重力、推力和m2的弹力,设对m1的弹力大小为N,
则竖直方向:m1g=Ncosθ
水平方向:F-Nsinθ=m1a
以(m1+m2)组成的整体为研究的对象,它们 在竖直方向:N′=(m2+m1)g
水平方向:F-μN′=(m2+m1)a
联立以上方程得:F=μ(m1+m2)g+$\frac{({m}_{1}+{m}_{2})}{{m}_{1}}(F-{m}_{1}gtanθ)$
所以,为了维持长方形两部分不发生相对运动则F的允许取值范围是:μ(m1+m2)g<F≤μ(m1+m2)g+$\frac{({m}_{1}+{m}_{2})}{{m}_{1}}(F-{m}_{1}gtanθ)$
(3)当A、B与水平地面间光滑时,且又m1=m2=m时
若要二者一起做加速运动,则推力要大于摩擦力,即:F>0
当m1恰好要相对于m2发生运动时,F达到最大值.此时m1在竖直方向上不再受到地面的支持力,它只受到重力、推力和m2的弹力,设对m1的弹力大小为N,
则竖直方向:m1g=Ncosθ
水平方向:F-Nsinθ=m1a
以(m1+m2)组成的整体为研究的对象,它们 在竖直方向:N′=(m2+m1)g
水平方向:F-=(m2+m1)a
联立以上方程得:F=$\frac{({m}_{1}+{m}_{2})}{{m}_{1}}(F-{m}_{1}gtanθ)$
所以,为了维持长方形两部分不发生相对运动则F的允许取值范围是:0<F≤$\frac{({m}_{1}+{m}_{2})}{{m}_{1}}(F-{m}_{1}gtanθ)$
答:(1)A、B间的相互作用力为$\frac{{m}_{2}F}{({m}_{1}+{m}_{2})sinθ}$
(2)为维持A、B间不发生相对滑动,力F的取值范围为μ(m1+m2)g<F≤μ(m1+m2)g+$\frac{({m}_{1}+{m}_{2})}{{m}_{1}}(F-{m}_{1}gtanθ)$.
(3)当A、B与水平地面间光滑时,且又m1=m2=m时,则F的取值范围是0<F≤$\frac{({m}_{1}+{m}_{2})}{{m}_{1}}(F-{m}_{1}gtanθ)$
点评 该题考查牛顿第二定律应用中的临界问题,一定要找到题目的题眼,该题中为:当F达到最大值时,m恰好要相对于M发生运动时,此时m在竖直方向上不再受到地面的支持力.

 “蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下的一种极限运动.某人做蹦极运动,所受绳子拉力F的大小随时间t变化的情况如图所示.将蹦极过程近似为在竖直方向的运动,重力加速度为g.据图可知,此人在蹦极过程中t0时刻的加速度约为( )
“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节等处,从几十米高处跳下的一种极限运动.某人做蹦极运动,所受绳子拉力F的大小随时间t变化的情况如图所示.将蹦极过程近似为在竖直方向的运动,重力加速度为g.据图可知,此人在蹦极过程中t0时刻的加速度约为( )| A. | 5g | B. | 3g | C. | 2g | D. | g |

| A. | 滑块与木板间的动摩擦因数为μ1=0.4 | |
| B. | 木板与地面间的动摩擦因数为μ2=0.1 | |
| C. | 木板的长度为L=4m | |
| D. | 木板的质量为M=1.5kg |
 如图所示,放在斜面上的物块以加速度a沿斜面匀加速下滑,若在物块上再施加一竖直向下的恒力F,斜面始终静止,则( )
如图所示,放在斜面上的物块以加速度a沿斜面匀加速下滑,若在物块上再施加一竖直向下的恒力F,斜面始终静止,则( )| A. | 物块仍以加速度a匀加速下滑 | |
| B. | 物块将以大于a的加速度匀加速下滑 | |
| C. | 地面对斜面的摩擦力方向一直向左 | |
| D. | 地面对斜面的摩擦力先向左后向右 |
| A. | 运动员起跳后在空中运动过程受到合外力冲量大小为m$\sqrt{{v}_{0}^{2}+2gH}$+mv0 | |
| B. | 水对运动员阻力的冲量大小为m$\sqrt{{v}_{0}^{2}+2gH}$ | |
| C. | 运动员克服水的阻力做功为mgH+$\frac{1}{2}$mv02 | |
| D. | 运动员从起跳到入水后速度减为零的过程中机械能减少量为mg(H+h)+$\frac{1}{2}$mv02 |

 如图所示,一根轻弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体,质量为m,当盘静止时,弹簧的长度比自然长度伸长了L.今向下拉盘使弹簧再伸长△L后停止,然后松手放开,设弹簧总处在弹性限度以内,刚刚松开手时盘对物体的支持力等于多少?(已知重力加速度为g)
如图所示,一根轻弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体,质量为m,当盘静止时,弹簧的长度比自然长度伸长了L.今向下拉盘使弹簧再伸长△L后停止,然后松手放开,设弹簧总处在弹性限度以内,刚刚松开手时盘对物体的支持力等于多少?(已知重力加速度为g) 如图所示,水平传送带以加速度a0=2m/s2顺时针匀加速运转,当传送带初速度v0=2m/s在M轮的正上方,将一质量为m=2kg的物体轻放在传送带上.已知物体与传送带之间的动摩擦因数μ=0.4,两传动轮M?N之间的距离为L=10m.求:
如图所示,水平传送带以加速度a0=2m/s2顺时针匀加速运转,当传送带初速度v0=2m/s在M轮的正上方,将一质量为m=2kg的物体轻放在传送带上.已知物体与传送带之间的动摩擦因数μ=0.4,两传动轮M?N之间的距离为L=10m.求: 有半径R=1m的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}}{2}$m.求出射角.
有半径R=1m的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}}{2}$m.求出射角.