题目内容
5. 有半径R=1m的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}}{2}$m.求出射角.
有半径R=1m的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}}{2}$m.求出射角.
分析 当光从图示位置射入,经过二次折射后射出球体,对两次折射分析运用折射定律列式,结合几何知识可求出出射光线的折射角.
解答  解:设入射光线与$\frac{1}{4}$球体的交点为C,连接OC,OC即为入射点的法线.因此,图中的角α为入射角.过C点作球体水平表面的垂线,垂足为B.依题意,∠COB=α.
解:设入射光线与$\frac{1}{4}$球体的交点为C,连接OC,OC即为入射点的法线.因此,图中的角α为入射角.过C点作球体水平表面的垂线,垂足为B.依题意,∠COB=α.
根据几何知识可得:sinα=$\frac{h}{R}$=$\frac{\frac{\sqrt{3}}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
得:α=60°
设光线在C点的折射角为β,由折射定律得:n=$\frac{sinα}{sinβ}$
解得:β=30°
由几何关系知,光线在球体的竖直表面上的入射角 γ=30°.
再由折射定律得 $\frac{sinγ}{sinθ}$=$\frac{1}{n}$
因此sinθ=nsinγ=$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,
解得 θ=60°
答:出射角θ是60°.
点评 当光线从球体入射时,法线即是入射点与球心的连线;当光线射出球体时,法线与界面垂直.本题两次使用折射定律可求出结果.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
3. 在如图所示电路中,电源内阻不可忽略,开关S闭合后,在滑动变阻器R2的滑动端由a向b缓慢滑动的过程中,下列说法正确的是( )
在如图所示电路中,电源内阻不可忽略,开关S闭合后,在滑动变阻器R2的滑动端由a向b缓慢滑动的过程中,下列说法正确的是( )
 在如图所示电路中,电源内阻不可忽略,开关S闭合后,在滑动变阻器R2的滑动端由a向b缓慢滑动的过程中,下列说法正确的是( )
在如图所示电路中,电源内阻不可忽略,开关S闭合后,在滑动变阻器R2的滑动端由a向b缓慢滑动的过程中,下列说法正确的是( )| A. | 电压表的示数减小 | B. | 电流表的示数减小 | ||
| C. | 电容器C所带电荷量增大 | D. | 电阻R3中有从右向左的电流 |
13.一块水平放置的光滑板面中心开一小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,并使小球在板面上以半径r做匀速圆周运动.现开始缓缓增大拉力F,使小球半径逐渐减小,若已知拉力变为8F时,小球的运动半径减为$\frac{r}{2}$;在此过程中,绳子对小球做的功是( )
| A. | 0 | B. | $\frac{Fr}{2}$ | C. | 4Fr | D. | $\frac{3Fr}{2}$ |
20. 一质量为m的物体恰能沿倾斜角为30°的斜劈匀速下滑,现对物体施加一个与斜面成30°角斜向下的恒力F,F=2mg,斜劈始终保持静止,则( )
一质量为m的物体恰能沿倾斜角为30°的斜劈匀速下滑,现对物体施加一个与斜面成30°角斜向下的恒力F,F=2mg,斜劈始终保持静止,则( )
 一质量为m的物体恰能沿倾斜角为30°的斜劈匀速下滑,现对物体施加一个与斜面成30°角斜向下的恒力F,F=2mg,斜劈始终保持静止,则( )
一质量为m的物体恰能沿倾斜角为30°的斜劈匀速下滑,现对物体施加一个与斜面成30°角斜向下的恒力F,F=2mg,斜劈始终保持静止,则( )| A. | 物体以$\frac{2\sqrt{3}}{3}$g的加速度加速下滑 | B. | 物体仍沿斜劈匀速下滑 | ||
| C. | 地面对斜劈的摩擦力水平向左 | D. | 地面对斜劈的摩擦力为零 |
10. 如图所示,将若干匝线圈固定在光滑绝缘杆上,另一个金属环 套在杆上与线圈共轴,当合上开关时线圈中产生磁场,金属环就可被加速弹射出去.现在线圈左侧同一位置处,先后放置形状.大小相同的铜环和铝环(两环分别用横截面积相等的铜和铝导线制成),且铝的电阻率大于铜的电阻率,闭合开关S的瞬间,下列描述正确的是( )
如图所示,将若干匝线圈固定在光滑绝缘杆上,另一个金属环 套在杆上与线圈共轴,当合上开关时线圈中产生磁场,金属环就可被加速弹射出去.现在线圈左侧同一位置处,先后放置形状.大小相同的铜环和铝环(两环分别用横截面积相等的铜和铝导线制成),且铝的电阻率大于铜的电阻率,闭合开关S的瞬间,下列描述正确的是( )
 如图所示,将若干匝线圈固定在光滑绝缘杆上,另一个金属环 套在杆上与线圈共轴,当合上开关时线圈中产生磁场,金属环就可被加速弹射出去.现在线圈左侧同一位置处,先后放置形状.大小相同的铜环和铝环(两环分别用横截面积相等的铜和铝导线制成),且铝的电阻率大于铜的电阻率,闭合开关S的瞬间,下列描述正确的是( )
如图所示,将若干匝线圈固定在光滑绝缘杆上,另一个金属环 套在杆上与线圈共轴,当合上开关时线圈中产生磁场,金属环就可被加速弹射出去.现在线圈左侧同一位置处,先后放置形状.大小相同的铜环和铝环(两环分别用横截面积相等的铜和铝导线制成),且铝的电阻率大于铜的电阻率,闭合开关S的瞬间,下列描述正确的是( )| A. | 从左侧看环中感应电流沿顺时针方向 | |
| B. | 线圈沿轴向有伸长的趋势 | |
| C. | 铜环受到的安培力大于铝环受到的安培力 | |
| D. | 若金属环出现断裂,不会影响其向左弹射 |
17. 如图所示,三个完全相同的物体a、b、c叠放在粗糙水平桌面上,a的左端通过一根轻绳与质量m=3$\sqrt{3}$kg的小球相连,小球静止在固定的光滑半球形器皿中,在半球形器皿中的绳与水平方向的夹角为60°,且半球形器皿边沿与物体a间的轻绳水平.水平向右的力F=30N作用在b上,三个物体保持静止状态.取g=10m/s2,下列说法正确的是( )
如图所示,三个完全相同的物体a、b、c叠放在粗糙水平桌面上,a的左端通过一根轻绳与质量m=3$\sqrt{3}$kg的小球相连,小球静止在固定的光滑半球形器皿中,在半球形器皿中的绳与水平方向的夹角为60°,且半球形器皿边沿与物体a间的轻绳水平.水平向右的力F=30N作用在b上,三个物体保持静止状态.取g=10m/s2,下列说法正确的是( )
 如图所示,三个完全相同的物体a、b、c叠放在粗糙水平桌面上,a的左端通过一根轻绳与质量m=3$\sqrt{3}$kg的小球相连,小球静止在固定的光滑半球形器皿中,在半球形器皿中的绳与水平方向的夹角为60°,且半球形器皿边沿与物体a间的轻绳水平.水平向右的力F=30N作用在b上,三个物体保持静止状态.取g=10m/s2,下列说法正确的是( )
如图所示,三个完全相同的物体a、b、c叠放在粗糙水平桌面上,a的左端通过一根轻绳与质量m=3$\sqrt{3}$kg的小球相连,小球静止在固定的光滑半球形器皿中,在半球形器皿中的绳与水平方向的夹角为60°,且半球形器皿边沿与物体a间的轻绳水平.水平向右的力F=30N作用在b上,三个物体保持静止状态.取g=10m/s2,下列说法正确的是( )| A. | 物体b受到物体a施加的一个大小为30N的静摩擦力,方向水平向右 | |
| B. | 桌面对物体a的摩擦力大小为0 | |
| C. | 物体c受到物体b施加的大小为30N的静摩擦力,方向水平向右 | |
| D. | 撤去力F的瞬间,三个物体一定会获得向左的加速度 |
14.洗衣机脱水时有一件衣物附在竖直筒壁上,如图所示,则下列说法正确的是( )


| A. | 衣物受到重力、筒壁对它的弹力、摩擦力及向心力共四个力的作用 | |
| B. | 衣物随筒壁做圆周运动的向心力由筒壁对它的弹力提供 | |
| C. | 筒的转速增大时,筒壁对衣物的摩擦力增大 | |
| D. | 筒的转速增大时,筒壁对衣物的弹力保持不变 |
15.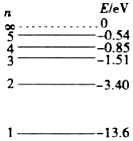 按照玻尔的理论,氢原子的能级是氢原子处于各个定态时的能量值,它包括氢原子系统的电势能和电子在轨道上运动的动能,能级图如图所示.当大量氢原子从n=4的能级向低能级跃迁时,下列说法正确的是( )
按照玻尔的理论,氢原子的能级是氢原子处于各个定态时的能量值,它包括氢原子系统的电势能和电子在轨道上运动的动能,能级图如图所示.当大量氢原子从n=4的能级向低能级跃迁时,下列说法正确的是( )
 按照玻尔的理论,氢原子的能级是氢原子处于各个定态时的能量值,它包括氢原子系统的电势能和电子在轨道上运动的动能,能级图如图所示.当大量氢原子从n=4的能级向低能级跃迁时,下列说法正确的是( )
按照玻尔的理论,氢原子的能级是氢原子处于各个定态时的能量值,它包括氢原子系统的电势能和电子在轨道上运动的动能,能级图如图所示.当大量氢原子从n=4的能级向低能级跃迁时,下列说法正确的是( )| A. | 电子的动能增加,氢原子系统的总能量增加 | |
| B. | 氢原子系统的电势能减小,总能量减少 | |
| C. | 氢原子可能辐射4种不同波长的光 | |
| D. | 从n=4到n=1发出的光的波长最长 |
 如图所示,A、B两物体的质量分别是m1和m2,其接触面光滑,与水平面的夹角为θ,若A、B与水平地面的动摩擦系数都是μ,用水平力F推A,使A、B一起加速运动,求:
如图所示,A、B两物体的质量分别是m1和m2,其接触面光滑,与水平面的夹角为θ,若A、B与水平地面的动摩擦系数都是μ,用水平力F推A,使A、B一起加速运动,求: