题目内容
10. 如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法正确的是(重力加速度为g)( )
如图所示,将质量为2m的重物悬挂在轻绳的一端,轻绳的另一端系一质量为m的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为d.现将小环从与定滑轮等高的A处由静止释放,当小环沿直杆下滑距离也为d时(图中B处),下列说法正确的是(重力加速度为g)( )| A. | 环与重物组成的系统机械能守恒 | |
| B. | 小环到达B处时,重物上升的高度也为d | |
| C. | 小环在B处的速度与重物上升的速度大小之比等于$\frac{\sqrt{2}}{2}$ | |
| D. | 小环在B处的速度时,环的速度为$\sqrt{(3-2\sqrt{2})gd}$ |
分析 环刚开始释放时,重物的加速度为零,根据牛顿第二定律判断绳子的拉力大小.根据数学几何关系求出环到达B处时,重物上升的高度.对B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,从而求出环在B处速度与重物的速度之比.环和重物组成的系统,机械能守恒.
解答 解:A、由于小环和重物只有重力做功,故系统机械能守恒,故A正确;
B、结合几何关系可知,重物上升的高度:h=$\frac{d}{cos45°}-d$=($\sqrt{2}$-1)d,故B错误;
C、两个物体沿着绳子方向的分速度,故:v环cos45°=vG,故环在B处的速度与重物上升的速度大小之比为$\sqrt{2}$:1,故C错误;
D、小环和重物系统机械能守恒,故:mgd=$\frac{1}{2}$mv环2+$\frac{1}{2}$(2m)vG2+(2m)gh;联立解得:v环=$\sqrt{(3-2\sqrt{2})gd}$,故D正确;
故选:AD.
点评 解决本题的关键知道系统机械能守恒,知道环沿绳子方向的分速度的等于重物的速度,要注意重物上升的高度不等于d,应由几何关系求解h.

练习册系列答案
相关题目
1.下述说法正确的是( )
| A. | 在以点电荷为球心,r为半径的球面上,各点的场强都相同 | |
| B. | 沿电场线方向,场强一定越来越小 | |
| C. | 电场线与电荷运动的轨迹是一致的 | |
| D. | 电场强度是反映电场本身特性的物理量,与是否存在试探电荷无关 |
18.在平直轨道上行驶的火车初速度为20m/s,关闭油门后前进50m停止,求火车速度减小过程中加速度的大小为( )
| A. | 2 m/s2 | B. | 4 m/s2 | C. | 6 m/s2 | D. | 8 m/s2 |
5.关于参考系的选取,下列说法正确的是( )
| A. | 参考系必须选取静止不动的物体 | |
| B. | 参考系必须是和地面联系在一起的 | |
| C. | 地球才是最理想的参考系 | |
| D. | 只有选择好了参考系,物体的运动情况才能确定 |
15. 如图,质量分别为m1=1.0kg和m2=2.0kg的弹性小球a、b,用轻绳紧紧的把它们捆在一起,使它们发生微小的形变.该系统以速度v0=0.10m/s沿光滑水平面向右做直线运动.某时刻轻绳突然自动断开,断开后两球仍沿原直线运动.经过时间t=5.0s后,测得两球相距s=4.5m,则下列说法正确的是( )
如图,质量分别为m1=1.0kg和m2=2.0kg的弹性小球a、b,用轻绳紧紧的把它们捆在一起,使它们发生微小的形变.该系统以速度v0=0.10m/s沿光滑水平面向右做直线运动.某时刻轻绳突然自动断开,断开后两球仍沿原直线运动.经过时间t=5.0s后,测得两球相距s=4.5m,则下列说法正确的是( )
 如图,质量分别为m1=1.0kg和m2=2.0kg的弹性小球a、b,用轻绳紧紧的把它们捆在一起,使它们发生微小的形变.该系统以速度v0=0.10m/s沿光滑水平面向右做直线运动.某时刻轻绳突然自动断开,断开后两球仍沿原直线运动.经过时间t=5.0s后,测得两球相距s=4.5m,则下列说法正确的是( )
如图,质量分别为m1=1.0kg和m2=2.0kg的弹性小球a、b,用轻绳紧紧的把它们捆在一起,使它们发生微小的形变.该系统以速度v0=0.10m/s沿光滑水平面向右做直线运动.某时刻轻绳突然自动断开,断开后两球仍沿原直线运动.经过时间t=5.0s后,测得两球相距s=4.5m,则下列说法正确的是( )| A. | 刚分离时,a球的速度大小为0.7m/s | |
| B. | 刚分离时,b球的速度大小为0.2m/s | |
| C. | 刚分离时,a、b两球的速度方向相同 | |
| D. | 两球分开过程中释放的弹性势能为0.27J |
2.一根电阻丝,在时间t内通过2C的电量时,消耗的电能为8J.若该电阻丝在时间内$\frac{t}{2}$通过4C的电量时,电阻丝上所加的电压U和消耗的电能E各是( )
| A. | U=8 V,E=16 J | B. | U=16 V,E=16 J | C. | U=8 V,E=32 J | D. | U=16 V,E=64 J |
 某电动机与灯泡连接电路如图所示.现 K1闭合(灯泡亮),K2断开,电流表读数为 5A;若保持 K1闭合,再将 K2关闭(电动机启动),电流表读数为 20A.已知电源电动势 E=12V,内阻 r=0.4Ω,电流表内阻不计,假设灯泡电阻恒定.求:因电动机启动,灯泡的电功率降低了多少?
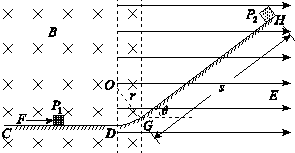
某电动机与灯泡连接电路如图所示.现 K1闭合(灯泡亮),K2断开,电流表读数为 5A;若保持 K1闭合,再将 K2关闭(电动机启动),电流表读数为 20A.已知电源电动势 E=12V,内阻 r=0.4Ω,电流表内阻不计,假设灯泡电阻恒定.求:因电动机启动,灯泡的电功率降低了多少? 质量为0.1g的小环带5×10-4C电荷量的负电荷,套在一根足够长的绝缘杆上,置于B=0.5T的匀强磁场中,磁场方向垂直于纸面向里与绝缘杆垂直如图所示,杆与水平方向成37°角,环与杆间的动摩擦因素为μ=0.40,求小环由静止开始下滑的最大加速度和最大速度.(磁场范围足够大,g=10m/s)
质量为0.1g的小环带5×10-4C电荷量的负电荷,套在一根足够长的绝缘杆上,置于B=0.5T的匀强磁场中,磁场方向垂直于纸面向里与绝缘杆垂直如图所示,杆与水平方向成37°角,环与杆间的动摩擦因素为μ=0.40,求小环由静止开始下滑的最大加速度和最大速度.(磁场范围足够大,g=10m/s)