题目内容
1. 如图所示,竖直平面内有一光滑圆弧轨道,其半径为R,平台与轨道的最高点等高,一小球从平台边缘的A处水平射出,恰能沿圆弧轨道上的P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为45°,试求:
如图所示,竖直平面内有一光滑圆弧轨道,其半径为R,平台与轨道的最高点等高,一小球从平台边缘的A处水平射出,恰能沿圆弧轨道上的P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为45°,试求:(1)小球从平台上的A点射出时的速度v0;
(2)小球从平台上射出点A到圆轨道入射点P之间的距离l;
(3)小球能否沿轨道通过圆弧的最高点?请说明理由.
分析 (1)恰好从光滑圆弧ABC的A点的切线方向进入圆弧,说明到到A点的速度vA方向与水平方向的夹角为θ,这样可以求出初速度v0;
(2)平抛运动水平方向做匀速直线运动,竖直方向做自由落体运动,根据平抛运动的基本规律求出P点与A点的水平距离和竖直距离,并进行合成求出位移大小;
(3)设小球能到达D点,根据机械能守恒定律求得D点速度,再运用牛顿第二定律和圆周运动知识求解
解答 解:(1)小球从A到P的高度差为:
h=R(1+cos45°)=($\frac{\sqrt{2}}{2}$+1)R,
小球做平抛运动,有:h=$\frac{1}{2}$gt2,
则小球在P点的竖直分速度为:vy=gt=$\sqrt{(2+\sqrt{2})gR}$.
把小球在P点的速度分解可得v0=vy,所以小球平抛初速度为:v0=$\sqrt{(2+\sqrt{2})gR}$
(2)小球平抛下降高度为:h=$\frac{1}{2}$vy•t,
水平射程为:s=v0t=2h,
故A、P间的距离为:l=$\sqrt{{h}^{2}+{s}^{2}}$=$\sqrt{5}$h=($\sqrt{5}$+$\frac{1}{2}$$\sqrt{10}$)R.
(3)小球从A到达Q时,根据机械能守恒定律可得:vQ=v0=$\sqrt{(2+\sqrt{2})gR}$>$\sqrt{gR}$,所以小球能通过圆弧轨道的最高点.
答:(1)小球从平台上的A点射出时的速度为$\sqrt{(2+\sqrt{2})gR}$;
(2)小球从平台上射出点A到圆轨道入射点P之间的距离为($\sqrt{5}$+$\frac{1}{2}$$\sqrt{10}$)R;
(3)小球能沿轨道通过圆弧的最高点,根据机械能守恒定律可得$\sqrt{(2+\sqrt{2})gR}$>$\sqrt{gR}$,所以小球能通过圆弧轨道的最高点.
点评 恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,这是解这道题的关键,理解了这句话就可以求得小球的末速度,本题很好的把平抛运动和圆周运动结合在一起运用机械能守恒解决,能够很好的考查学生的能力,是道好题.本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外,求速度的问题,动能定理不失为一种好的方法.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 中轨道卫星的线速度小于高轨道卫星的线速度 | |
| B. | 中轨道卫星的角速度小于同步卫星的角速度 | |
| C. | 若一周期为8h的中轨道卫星某时刻在同步卫星的正下方,则经过24h仍在该同步卫星的正下方 | |
| D. | 高轨道卫星的向心加速度小于同步卫星的向心加速度 |

| A. | 若木块静止,则木块受到的静摩擦力大小等于mg,方向竖直向上 | |
| B. | 若木块静止,当F增大时,木块受到的静摩擦力随之增大 | |
| C. | 若木块沿墙壁向下运动,则墙壁对木块的摩擦力大小为μmg | |
| D. | 若开始时木块静止.当撤去F,木块沿墙壁下滑时,木块不受滑动摩擦力作用 |
| A. | 光敏电阻其阻值随光照的强弱而改变 | |
| B. | 霍尔元件能够把温度这个热学量转化为电压这个电学量 | |
| C. | 热敏电阻是用金属铂制成的,化学稳定性较好,灵敏度较差 | |
| D. | 金属热电阻的化学稳定性较差,但灵敏度高 |
| A. | 如果地球没有自转,只要采取适当的发射速度和发射角度,也可以发射地球同步卫星 | |
| B. | 小船在水速较小的河中横渡,并使船头始终垂直河岸航行,到达河中间时突然上游来大水使水流速度加快,则小船要用更长的时间才能到达对岸 | |
| C. | 一个物体以0.5g竖直下落了高度h,机械能减少0.5mgh | |
| D. | 无论宏观物体还是微观物体,无论高速运动还是低速运动,都可以运用牛顿运动规律处理 |
 如图所示,在“验证力的平行四边形定则”实验中,用力F1、F2通过弹簧测力器拉动橡皮条端点的小圆环,使橡皮条再次伸长,实验中必须确保( )
如图所示,在“验证力的平行四边形定则”实验中,用力F1、F2通过弹簧测力器拉动橡皮条端点的小圆环,使橡皮条再次伸长,实验中必须确保( )| A. | F大小等于F1大小与F2大小之和 | |
| B. | F大小等于F1大小与F2大小之差 | |
| C. | 橡皮条的伸长量不能超过弹性限度 | |
| D. | 两次橡皮条伸长量均应使小圆环处于同一位置 |
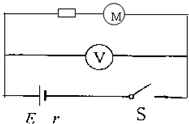 宜宾市小科学家协会的一位同学设计了一台玩具车,其内部结构的简化电路图如图所示.电源电动势为E,内阻r=1Ω,直流电动机M的线圈电阻R0=1Ω,与R=1Ω的保护电阻串联后接入电路中.电动机正常工作时,通过电动机的电流强度I=1A,电压表示数U=11V.求:
宜宾市小科学家协会的一位同学设计了一台玩具车,其内部结构的简化电路图如图所示.电源电动势为E,内阻r=1Ω,直流电动机M的线圈电阻R0=1Ω,与R=1Ω的保护电阻串联后接入电路中.电动机正常工作时,通过电动机的电流强度I=1A,电压表示数U=11V.求: 如图所示,斜面倾角为θ=30°,一弹簧下端与固定挡板连接,上端与一个质量为2kg的物体相连,物体在斜面上静止不动.弹簧原长为10cm,现在的长度为8cm.(g=10m/s2)
如图所示,斜面倾角为θ=30°,一弹簧下端与固定挡板连接,上端与一个质量为2kg的物体相连,物体在斜面上静止不动.弹簧原长为10cm,现在的长度为8cm.(g=10m/s2) 在“研究平抛物体运动”的实验中,可以描绘平抛物体运动轨迹和求物体的平抛初速度.
在“研究平抛物体运动”的实验中,可以描绘平抛物体运动轨迹和求物体的平抛初速度.