题目内容
10．
2016年里约奥运会，中国选手宫金杰、钟天使获场地自行车团体竞速冠军．场地自行车没有车闸，但在弯道处不需要刹车减速也能安全通过，这是因为跑道建成内低外高的侧斜面，且整条赛道的坡度由内向外逐渐变陡，即倾角θ不断增大，如图所示，若运动员转弯时所需的向心力完全由重力mg和支持力FN的合力来提供，则（ ）| A． | 转弯的过程中支持力FN=mgtanθ | B． | 转弯的过程中支持力FN=mgcosθ | ||
| C． | 转弯时在内侧轨道的选手速度大 | D． | 转弯时在外侧轨道的选手速度大 |
分析 运动员转弯时所需的向心力完全由重力mg和支持力FN的合力来提供，根据平行四边形定则求出支持力的大小，结合合力提供向心力得出速度的表达式，从而确定内侧还是外侧速度大．
解答 解：AB、根据平行四边形定则知，转弯过程中的支持力为：${F}_{N}=\frac{mg}{cosθ}$，故AB错误．
CD、根据$mgtanθ=m\frac{{v}^{2}}{R}$得：v=$\sqrt{gRtanθ}$，内侧倾角较小，速度较小，外侧倾角较大，速度较大，故C错误，D正确．
故选：D．
点评 解决本题的关键知道运动员转弯时向心力的来源，结合牛顿第二定律进行求解，基础题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
1．
如图所示，一平行导轨水平放置，距为d，一端连接电阻R，磁场的磁感应强度为B，方向与导轨所在平面垂直．一根光滑金属棒ab与导轨成θ角放置，金属棒与导轨的电阻不计．当金属棒沿平行于导轨的方向以速度v匀速滑行时，则作用于金属棒的拉力的大小与方向是（ ）
如图所示，一平行导轨水平放置，距为d，一端连接电阻R，磁场的磁感应强度为B，方向与导轨所在平面垂直．一根光滑金属棒ab与导轨成θ角放置，金属棒与导轨的电阻不计．当金属棒沿平行于导轨的方向以速度v匀速滑行时，则作用于金属棒的拉力的大小与方向是（ ）| A． | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{R}$，方向是水平向右 | |
| B． | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{R}$，方向是垂直金属棒斜向下 | |
| C． | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{Rsinθ}$，方向是垂直金属棒斜向下 | |
| D． | 金属棒的拉力大小是$\frac{{B}^{2}{d}^{2}v}{Rsinθ}$，方向是水平向右 |
如图所示，底边在x轴上，长为3L，高为L，底角为45°的等腰梯形内分布着垂直纸面向外的匀强磁场．t=0时有一边长也为L的正方形导线框恰好位于图示位置沿x轴正方向匀速穿过该磁场区域．若以顺时针方向为导线框中电流的正方向，在下面四幅图中能正确表示导线框中电流和位移关系的是（ ）
5．
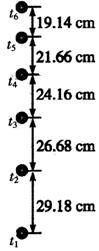某同学利用频闪照相法验证机械能守恒定律．该同学将一质量为m=0.2kg的小球竖直上抛，获得部分运动过程的频闪照片如图所示．已知图中所标数据为实际距离，频闪仪每隔0.05s闪光一次，当地重力加速度为10m/s2．该同学通过计算得到不同时刻的速度如下表：
（1）根据频闪照片上的数据计算t5时刻小球的速度v5=4.08m/s；
（2）从t2时刻到t5时刻，小球重力势能的增加量△Ep=1.45J，动能的减少量△Ek=1.46J． 在误差允许的范围内，若△Ep与△Ek近似相等，就能验证机械能守恒定律．（以上结果均保留三位有效数字）
某同学利用频闪照相法验证机械能守恒定律．该同学将一质量为m=0.2kg的小球竖直上抛，获得部分运动过程的频闪照片如图所示．已知图中所标数据为实际距离，频闪仪每隔0.05s闪光一次，当地重力加速度为10m/s2．该同学通过计算得到不同时刻的速度如下表：| 时刻 | t2 | t3 | t4 | t5 |
| 速度（m/s） | 5.59 | 5.08 | 4.58 |
（2）从t2时刻到t5时刻，小球重力势能的增加量△Ep=1.45J，动能的减少量△Ek=1.46J． 在误差允许的范围内，若△Ep与△Ek近似相等，就能验证机械能守恒定律．（以上结果均保留三位有效数字）
15．
如图，从固定斜面顶端将小球分别以v0和2v0水平抛出，小球仍落在斜面上，两次小球平抛运动时间分别为t1、t2，水平位移分别为x1、x2，竖直下落高度分别为h1、h2．则下列关系正确的是 （ ）
如图，从固定斜面顶端将小球分别以v0和2v0水平抛出，小球仍落在斜面上，两次小球平抛运动时间分别为t1、t2，水平位移分别为x1、x2，竖直下落高度分别为h1、h2．则下列关系正确的是 （ ）| A． | 4t1=t2 | B． | 4x1=x2 | C． | h1=h2 | D． | 2h1=h2 |
2．
静止在水平地面的物块，受到水平向右的拉力F的作用，F随时间t的变化情况如图所示．设物块与地面间的最大静摩擦力与滑动摩擦力大小相等，且为1N，则（ ）
静止在水平地面的物块，受到水平向右的拉力F的作用，F随时间t的变化情况如图所示．设物块与地面间的最大静摩擦力与滑动摩擦力大小相等，且为1N，则（ ）| A． | 0～1s时间内，物块的加速度逐渐增大 | |
| B． | 第3s末，物块的速度最大 | |
| C． | 第3s末，物块的加速度为零 | |
| D． | 第7s末，物块的动能最大 |
19．
在水平面上固定两个相互紧靠的三角形斜面，将a、b、c三个小球从左边斜面的顶点以不同的初速度向右水平抛出，落在斜面上时其落点如图所示，小球a落点距水平面的高度最低．下列判断正确的是（ ）
在水平面上固定两个相互紧靠的三角形斜面，将a、b、c三个小球从左边斜面的顶点以不同的初速度向右水平抛出，落在斜面上时其落点如图所示，小球a落点距水平面的高度最低．下列判断正确的是（ ）| A． | 小球c的初速度最小 | |
| B． | 小球a的飞行时间最长 | |
| C． | 小球c的整个飞行过程速度变化量最大 | |
| D． | 若减小小球a的初速度，其整个飞行过程速度变化量增大 |