题目内容
19．张华将小皮球投射到平面镜上，经平面镜反弹击中目标区内的物体，他沿图甲CO方向射球（填OA、OB或OC），最有可能击中目标；用激光笔沿图乙AO方向照射，最有可能瞄中水中的玩具鱼（填AO、BO或CO）．
分析 甲图中，把O看作点光源，目标看成反射光线经过的点，根据光的反射定律分析．
乙图中，根据光的折射定律分析折射角和入射角的关系，从而作出判断．
解答 
解：甲图中：把O看作点光源，分别过入射点E、F、H作法线，可得入射角．由光的反射定律可知反射角等于入射角，从而作出反射光线．由图可知，只有过入射点E的反射光线才能经过目标区，其他点的反射光线不经过目标区，所以他沿图甲CO方向射球，最有可能击中目标．
乙图中：光线在水面折射时，折射角小于入射角，由折射定律知，用激光笔沿图乙AO方向照射，最有可能瞄中水中的玩具鱼．
故答案为：CO、AO
点评 解决本题的关键要掌握光折射定律和反射定律，并能灵活用来分析实际问题．甲图中能熟练运用光路可逆原理分析．
练习册系列答案
能考试全能100分系列答案
相关题目
9．
有一边长分別为L和2L的矩形导体框，导体框的总电阻为R，让导休框在磁慼应强度为B的匀强磁场中以恒定角速度ω绕两短边中点为轴旋转，如图所示（ ）
有一边长分別为L和2L的矩形导体框，导体框的总电阻为R，让导休框在磁慼应强度为B的匀强磁场中以恒定角速度ω绕两短边中点为轴旋转，如图所示（ ）| A． | 导体框的发热功率$\frac{2{B}^{2}{l}^{4}{ω}^{2}}{R}$ | |
| B． | 导体框转到图示位置时，某一长边两端电压$\frac{1}{3}B{l}^{2}ω$ | |
| C． | 从图示位置开始线圈转过60°的过程中通过电阻R的电量$\frac{\sqrt{3}B{L}^{2}}{2（R+r）}$ | |
| D． | 从图示位置开始，线圈转过60°时的电动势是Bl2ω |
10．在如图甲所示的电阻R上加上如图乙所示的交变电压，电表为理想交变电表（ ）
| A． | 交变电压周期是0.02s | |
| B． | 电压表读数为220V | |
| C． | 0.01s时，电流表读数为0 | |
| D． | 通过R的电流表达式为i=$\frac{220}{R}$sin100πt（A） |
7．
如图所示，直角玻璃三棱镜置于空气中，已知棱镜的折射率n=$\sqrt{2}$，∠A=60°，一束极细的光从AC的中点D垂直AC面入射，AD=a，光从棱镜第一次射入空气时的折射角θ和光从进入棱镜到它第一次射出空气所经历的时间t为（ ）
如图所示，直角玻璃三棱镜置于空气中，已知棱镜的折射率n=$\sqrt{2}$，∠A=60°，一束极细的光从AC的中点D垂直AC面入射，AD=a，光从棱镜第一次射入空气时的折射角θ和光从进入棱镜到它第一次射出空气所经历的时间t为（ ）| A． | 30°，$\frac{{5\sqrt{6}a}}{3c}$ | B． | 45°，$\frac{{5\sqrt{6}a}}{3c}$ | C． | 30°，$\frac{{5\sqrt{3}a}}{3c}$ | D． | 45°，$\frac{{5\sqrt{3}a}}{3c}$ |
11．
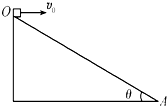如图所示，足够长斜面OA的倾角为θ，固定在水平地面上，现从顶点O以速度v0平抛一小球，不计空气阻力，重力加速度为g，求小球在飞行过程中与斜面之间的最远距离（ ）•
如图所示，足够长斜面OA的倾角为θ，固定在水平地面上，现从顶点O以速度v0平抛一小球，不计空气阻力，重力加速度为g，求小球在飞行过程中与斜面之间的最远距离（ ）•| A． | $\frac{{v}_{0}sinθ}{2g}$ | B． | $\frac{{{v}_{0}}^{2}}{2g}$ | ||
| C． | $\frac{{{v}_{0}}^{2}sinθ}{2gcosθ}$ | D． | $\frac{{{v}_{0}}^{2}si{n}^{2}θ}{2gcosθ}$ |
10．列关于物理学思想和方法的叙述错误的是（ ）
| A． | 在推导匀变速直线运动位移公式时，把整个运动过程划分成很多小段，每一小段近似看作匀速直线运动，再把各小段位移相加，这里运用了微元法 | |
| B． | 探究加速度与力和质量关系的实验运用了控制变量法 | |
| C． | 当物体的运动时间△t趋近于0时，△t时间内的平均速度可看成瞬时速度运用了等效替代法 | |
| D． | 奥斯特发现电生磁到法拉第发现磁生电的过程中运用了逆向思维法 |