题目内容
14.如图甲所示,两个带正电的小球A、B套在一个倾斜的光滑直杆上,两球均可视为点电荷,其中A球固定,带电量QA=2×10-4C,B球的质量为m=0.1kg.以A为坐标原点,沿杆向上建立直线坐标系,A、B球与地球所组成的系统总势能(重力势能与电势能之和)随位置x的变化规律如图中曲线Ⅰ所示,直线Ⅱ为曲线I的渐近线.图中M点离A点距离为6米.(g取10m/s2,静电力恒量k=9.0×109N•m2/C2.令A处所在平面为重力势能的零势能面,无穷远处为零电势能处).
(1)求杆与水平面的夹角θ;
(2)求B球的带电量QB;
(3)求M点电势φM;
(4)若B球以Ek0=4J的初动能从M点开始沿杆向上滑动,求B球运动过程中离A球的最近距离及此时B球的加速度.
分析 (1)由图运用数学知识得到 Ep=mgxsinθ=kx,从而的角度θ;
(2)由图乙中的曲线Ⅰ知,在x=6m出总势能最小,动能最大,该位置B受力平衡,根据平衡条件和库仑定律求解电荷量.
(3)根据电势和电势能关系求解电势;
(4)根据能量守恒和牛顿运动定律求解加速度a.
解答 解:(1)渐进线Ⅱ表示B的重力势能随位置的变化关系,即 Ep=mgxsinθ=kx
则 sinθ=$\frac{k}{mg}$=0.5 即 θ=30°;
(2)由图乙中的曲线Ⅰ知,在x=6m出总势能最小,动能最大,该位置B受力平衡
则有 mgsin30°=k$\frac{{Q}_{A}{Q}_{B}}{{x}^{2}}$
解得 QB=1×10-5C;
(3)M点的电势能 EPM=E总-EP=6-3=3J
则M点电势 φM=$\frac{{E}_{pM}}{{Q}_{B}}$=3×105V;
(4)在M点B球总势能为6J,根据能量守恒定律,当B的动能为零,总势能为10J,由曲线Ⅰ知B离A的最近距离为 x=2m.
k$\frac{{Q}_{A}{Q}_{B}}{{x}^{2}}$-mg=ma 解得a=40m/s2,方向沿杆向上;
答:
(1)杆与水平面的夹角θ为30°;
(2)B球的带电量QB是1×10-5C;
(3)M点电势φM是3×105V;
(4)若B球以Ek0=4J的初动能从M点开始沿杆向上滑动,B球运动过程中离A球的最近距离是2m,此时B球的加速度是40m/s2,方向沿杆向上.
点评 此题考查读图能量,注意选择合适的点,分析隐含的条件,同时要熟练应用牛顿运动定律和能量守恒解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图,一跨过定滑轮的足够长细绳两端分别连接A、B两物体,质量mA<mB初始时,用手托着物体B,使系统处于静止状态,现突然撤去手的作用,不计绳与滑轮间的摩擦,重力加速度为g,则在A向上运动的过程中,细绳拉力大小一定为( )
如图,一跨过定滑轮的足够长细绳两端分别连接A、B两物体,质量mA<mB初始时,用手托着物体B,使系统处于静止状态,现突然撤去手的作用,不计绳与滑轮间的摩擦,重力加速度为g,则在A向上运动的过程中,细绳拉力大小一定为( )
 如图,一跨过定滑轮的足够长细绳两端分别连接A、B两物体,质量mA<mB初始时,用手托着物体B,使系统处于静止状态,现突然撤去手的作用,不计绳与滑轮间的摩擦,重力加速度为g,则在A向上运动的过程中,细绳拉力大小一定为( )
如图,一跨过定滑轮的足够长细绳两端分别连接A、B两物体,质量mA<mB初始时,用手托着物体B,使系统处于静止状态,现突然撤去手的作用,不计绳与滑轮间的摩擦,重力加速度为g,则在A向上运动的过程中,细绳拉力大小一定为( )| A. | T=mAg | B. | T=(mB-mA)g | ||
| C. | T=$\frac{{m}_{B}({m}_{B}-{m}_{A})g}{{m}_{A}+{m}_{B}}$ | D. | T=$\frac{2{m}_{A}{m}_{B}g}{{m}_{A}+{m}_{B}}$ |
5. 如图,拖着旧橡胶轮胎跑是身体耐力训练的一种有效方法.如果某受训者拖着轮胎在水平直道上跑了100m,那么下列说法正确的是( )
如图,拖着旧橡胶轮胎跑是身体耐力训练的一种有效方法.如果某受训者拖着轮胎在水平直道上跑了100m,那么下列说法正确的是( )
 如图,拖着旧橡胶轮胎跑是身体耐力训练的一种有效方法.如果某受训者拖着轮胎在水平直道上跑了100m,那么下列说法正确的是( )
如图,拖着旧橡胶轮胎跑是身体耐力训练的一种有效方法.如果某受训者拖着轮胎在水平直道上跑了100m,那么下列说法正确的是( )| A. | 轮胎受到的重力做了正功 | B. | 轮胎受到的拉力不做功 | ||
| C. | 轮胎受到地面的支持力做了正功 | D. | 轮胎受到地面的摩擦力做了负功 |
5.第一个测出元电荷数值的科学家是( )
| A. | 库伦 | B. | 法拉第 | C. | 密立根 |
 如图所示,质量m1=0.3kg的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求:
如图所示,质量m1=0.3kg的小车静止在光滑的水平面上,车长L=1.5m,现有质量m2=0.2kg可视为质点的物块,以水平向右的速度v0=2m/s从左端滑上小车,最后在车面上某处与小车保持相对静止.物块与车面间的动摩擦因数μ=0.5,取g=10m/s2,求: 如图所示,粗细均匀的电阻为r的金属圆环,放在图示的匀强磁场中,磁感应强度为B,圆环直径为L,长为L、电阻也为r的金属棒ab放在圆环上,以v0向左运动到图示圆心位置时,金属棒两端的电势差的绝对值为$\frac{1}{5}$BLv0,通过金属棒的电流的方向是a到b.
如图所示,粗细均匀的电阻为r的金属圆环,放在图示的匀强磁场中,磁感应强度为B,圆环直径为L,长为L、电阻也为r的金属棒ab放在圆环上,以v0向左运动到图示圆心位置时,金属棒两端的电势差的绝对值为$\frac{1}{5}$BLv0,通过金属棒的电流的方向是a到b.

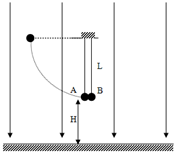 在空间足够大的方向竖直向下的匀强电场中两长为L的绝缘细线并列上端固定,另一端悬挂质量分别为mA和mB的带正电小球,带电量分别为qA和qB,且有$\frac{{q}_{A}}{{m}_{A}}$=$\frac{{q}_{B}}{{m}_{B}}$=k.平衡时,两小球刚好相接触并无弹力,距地面高度为H,现将A球拉离至与悬点等高处,使细线绷直,由静止释放,当A摆至最低点时与B球发生弹性碰撞,刚碰撞完的瞬间,系B球的细线突然被拉断.(不计两球间的库仑力,已知电场强度为E.)求:
在空间足够大的方向竖直向下的匀强电场中两长为L的绝缘细线并列上端固定,另一端悬挂质量分别为mA和mB的带正电小球,带电量分别为qA和qB,且有$\frac{{q}_{A}}{{m}_{A}}$=$\frac{{q}_{B}}{{m}_{B}}$=k.平衡时,两小球刚好相接触并无弹力,距地面高度为H,现将A球拉离至与悬点等高处,使细线绷直,由静止释放,当A摆至最低点时与B球发生弹性碰撞,刚碰撞完的瞬间,系B球的细线突然被拉断.(不计两球间的库仑力,已知电场强度为E.)求: