题目内容
17.有一宇宙飞船,以速度v接近某行星表面匀速飞行,测出运动的周期为T,已知引力常量为G,则可得( )| A. | 该行星的半径为$\frac{vT}{2π}$ | B. | 该行星的平均密度为$\frac{3π}{{G{T^2}}}$ | ||
| C. | 该行星的质量为$\frac{{4{π^2}v}}{{G{T^2}}}$ | D. | 该行星表面的重力加速度为$\frac{2πv}{T}$ |
分析 根据线速度与周期的关系求出行星的半径;根据万有引力提供向心力求出行星的质量,结合行星的体积求出行星的平均密度;根据行星的半径和行星质量的表达式求出行星的质量.根据万有引力等于重力求出行星表面的重力加速度.
解答 解:A、根据T=$\frac{2πR}{v}$知,行星的半径R=$\frac{vT}{2π}$,故A正确.
B、根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得,行星的质量M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,则行星的平均密度$ρ=\frac{M}{V}$=$\frac{\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4π{R}^{3}}{3}}=\frac{3π}{G{T}^{2}}$,故B正确.
C、由B选项知,行星的质量M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,R=$\frac{vT}{2π}$,解得M=$\frac{{v}^{3}T}{2πG}$,故C错误.
D、根据$G\frac{Mm}{{R}^{2}}=mg$得,g=$\frac{GM}{{R}^{2}}=\frac{4{π}^{2}R}{{T}^{2}}=\frac{4{π}^{2}}{{T}^{2}}•\frac{vT}{2π}=\frac{2πv}{T}$,故D正确.
故选:ABD.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力提供向心力,2、万有引力等于重力,并能灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.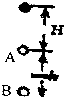 如图所示,以一定的初速度竖直向上从A点抛出一个小球,小球上升的最大的高度为H,假设空气阻力的大小恒为f,则从抛出至落到出发点下方h处的B点过程中,小球克服空气阻力做功和小球重力势能的变化量别为( )
如图所示,以一定的初速度竖直向上从A点抛出一个小球,小球上升的最大的高度为H,假设空气阻力的大小恒为f,则从抛出至落到出发点下方h处的B点过程中,小球克服空气阻力做功和小球重力势能的变化量别为( )
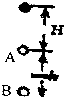 如图所示,以一定的初速度竖直向上从A点抛出一个小球,小球上升的最大的高度为H,假设空气阻力的大小恒为f,则从抛出至落到出发点下方h处的B点过程中,小球克服空气阻力做功和小球重力势能的变化量别为( )
如图所示,以一定的初速度竖直向上从A点抛出一个小球,小球上升的最大的高度为H,假设空气阻力的大小恒为f,则从抛出至落到出发点下方h处的B点过程中,小球克服空气阻力做功和小球重力势能的变化量别为( )| A. | f(2H+h);mgh | B. | -f(2H+h);-mgh | C. | -f(2H+h);mgh | D. | f(2H+h);-mgh |
8.自然界中有很多物体做曲线运动.在所有的曲线运动中,物体的( )
| A. | 速度一定改变 | B. | 动能一定改变 | ||
| C. | 重力势能一定不变 | D. | 机械能一定不变 |
12.一质点做速度逐渐增大的匀加速直线运动,在时间间隔t内位移为s,动能变为原来的4倍.该质点的加速度为( )
| A. | $\frac{s}{{t}^{2}}$ | B. | $\frac{3s}{2{t}^{2}}$ | C. | $\frac{2s}{3{t}^{2}}$ | D. | $\frac{4s}{{t}^{2}}$ |
2.质量是100g的物体从1.8m的高处落下,又弹到1.25m处.则重力对物体做功和重力势能变化各是( )
| A. | 1.8J,增加0.55J | B. | 1.8J,减小1.8J | C. | 0.55J,增加0.55J | D. | 0.55J,减小0.55J |
5.平抛运动的物体( )
| A. | 做匀变速曲线运动,每秒内速度变化的大小相等 | |
| B. | 做匀变速曲线运动,每秒内速度变化的方向不同 | |
| C. | 水平飞行的距离只与初速度大小有关 | |
| D. | 飞行时间只与下落的高度有关 |
 如图所示,质量m=1kg的小物体(可视为质点)从光滑曲面上高度H=0.45m处静止释放,到达底端时水平进入轴心距离L=1m的水平传送带,已知物体与传送带间的动摩擦因数为μ=0.4(取g=10m/s2).求:
如图所示,质量m=1kg的小物体(可视为质点)从光滑曲面上高度H=0.45m处静止释放,到达底端时水平进入轴心距离L=1m的水平传送带,已知物体与传送带间的动摩擦因数为μ=0.4(取g=10m/s2).求:
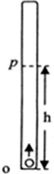 如图所示是一种测量重力加速度g的装置.在某星球上,将真空长直管沿竖直方向放置,管内小球以某一初速度自O点竖直上抛,经t时间上升到最高点,OP间的距离为h,已知引力常量为G,星球的半径为R.求:
如图所示是一种测量重力加速度g的装置.在某星球上,将真空长直管沿竖直方向放置,管内小球以某一初速度自O点竖直上抛,经t时间上升到最高点,OP间的距离为h,已知引力常量为G,星球的半径为R.求: