题目内容
质量M=3.0×106kg的列车，在恒定的额定功率下，沿平直的轨道由静止开始出发，在运动的过程中受到的阻力为f．列车达到最大行驶速度v=30m/s后，某时刻司机得知前方x=1.5×103m处的轨道被毁坏，便立即紧急刹车，刹车时汽车受到的阻力为原来的9倍，结果列车正好到达轨道毁坏处停下．求：
（1）列车刹车过程中加速度的大小；
（2）列车的额定功率P．
（1）列车刹车过程中加速度的大小；
（2）列车的额定功率P．
分析：（1）根据匀变速直线运动的速度位移公式求出列车刹车过程中的加速度大小．
（2）根据牛顿第二定律求出刹车过程中的阻力，从而得出匀速行驶的阻力大小，结合P=Fv求出列车的额定功率．
（2）根据牛顿第二定律求出刹车过程中的阻力，从而得出匀速行驶的阻力大小，结合P=Fv求出列车的额定功率．
解答：解：（1）刹车后列车做匀减速运动直到停下，设加速度大小为a
v2=2ax
代入数据联立解得：a=0.3m/s2
（2）刹车后列车水平方向受二力作用，由牛顿第二定律：
9f=Ma f=1.0×105N
当列车达到最大速度时，加速度为零，即牵引力F=f
所以：P=Fv
代入数据得：P=3.0×106W
答：（1）列车刹车过程中加速度的大小为0.3m/s2；
（2）列车的额定功率为3.0×106W．
v2=2ax
代入数据联立解得：a=0.3m/s2
（2）刹车后列车水平方向受二力作用，由牛顿第二定律：
9f=Ma f=1.0×105N
当列车达到最大速度时，加速度为零，即牵引力F=f
所以：P=Fv
代入数据得：P=3.0×106W
答：（1）列车刹车过程中加速度的大小为0.3m/s2；
（2）列车的额定功率为3.0×106W．
点评：本题考查了牛顿第二定律和运动学公式的综合，知道加速度是联系力学和运动学的桥梁．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，两块平行金属板MN、PQ竖直放置，两板间的电势差U=1.6×103 V，现将一质量m=3.0×10-2 kg、电荷量q=+4.0×10-5 C的带电小球从两板左上方的A点以初速度v0=4.0m/s水平抛出，已知A点距两板上端的高度h=0.45m，之后小球恰好从MN板上端内侧M点进入两板间匀强电场，然后沿直线运动到PQ板上的C点，不计空气阻力，取g=10m/s2，求：
如图所示，水平放置的平行板电容器的两极板M、N，接上直流电源．上极板M的中央有一小孔A，在A的正上方h处的B点，有一小油滴自由落下．已知小油滴的电量Q=3.5×10-14 C，质量m=3.0×10-9kg．当小油滴即将落到下极板时速度恰为零．两极板间的电势差U=6×105 V（不计空气阻力，g=10m/s2）求：?（1）两极板间的电场强度E；
如图所示，在真空室内x轴正半轴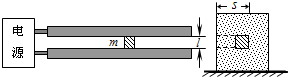
如图，竖直面内两根光滑平行金属导轨沿水平方向固定，其间安放金属滑块，滑块始终与导轨保持良好接触．电源提供的强电流经导轨、滑块、另一导轨流回电源．同时电流在两导轨之间形成较强的磁场（可近似看成匀强磁场），方向垂直于纸面，其强度与电流的大小关系为B=kI，比例常数k=2.5×10-6T/A．已知两导轨内侧间距l=1.5cm，滑块的质量m=3.0×10-2kg，滑块由静止开始沿导轨滑行S=5m后获得的发射速度v=3.0×103m/s（此过程可视为匀加速运动）．求：