Question

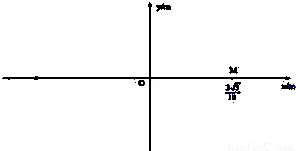
如图所示，在真空室内x轴正半轴M(

3 3

10

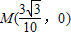，0)点固定一负的点电荷，电量Q=-6.4×10^-6C．点电荷左侧的电场分布以y轴为界限．在x轴负半轴远离原点某处有一粒子放射源不断沿x轴正向放射出速度相同的带正电的粒子．粒子质量m=3.0×10^-27kg，电量q=+3.2×10^-19C，速率v=3.2×10⁶m/s．为使带电粒子进入y轴右侧后作匀速圆周运动，最终打在位于x正半轴点电荷右侧的荧光屏上（未画出），可在y轴左侧加一个方向垂直纸面向外、圆心在x轴上的圆形匀强磁场区域，其磁感应强度B=0.30T．不计粒子重力，静电力常数K=9×10⁹N?m²/C²．求：
（1）所加圆形匀强磁场区域的圆心坐标．
（2）所加磁场的区域半径．

Answer 1

分析：（1）根据题意，粒子进入电场中做匀速圆周运动，库仑力提供向心力，根据牛顿第二定律求出粒子运动的半径，再根据几何关系求出所加圆形匀强磁场区域的圆心坐标．
（2）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，根据牛顿第二定律求出粒子运动的半径，再根据几何关系求出所加圆形匀强磁场区域的半径．

解答：解：（1）设粒子进入电场中做匀速圆周运动的轨道半径为r，
k

Qq

r2

=

mv2

r

r=

kQq

mv2

=0.6(m)

由题意可知：要使粒子进入电场时作匀速圆周运动，须满足粒子必须在N点进入电场（如图所示），且MN=r，进入电场时速度方向垂直于MN
由几何关系可得ON=0.3（m） 
OO′=

3

10

m磁场圆心坐标为(-

3

10

，0)
（2）设粒子在磁场中的运动轨道半径为R，Bqv=

mv2

R

R=

mv

Bq

=0.1(m)
如图所示：由几何关系可得所加磁场区域的半径R′=R×tan30°=

3

30

m
答：（1）所加圆形匀强磁场区域的圆心坐标(-

3

10

，0)．
（2）所加磁场的区域半径

3

30

m．

点评：该题中，带电粒子分别在匀强磁场中和在点电荷的电场中做匀速圆周运动，分别有洛伦兹力和库仑力提供向心力，动力学方程是解题 的关键．