题目内容
8. 如图甲所示,小轴正方向水平向右,y轴正方向竖直向上,在xOy平面内有与y轴平行的匀强电场在半径为R的圆形区域加有与xOy平面垂直的匀强磁场,在坐标原点O处放置一带电微粒发射装置.它可以连续不断地发射具有相同质量m、电荷量q(q>0)和初速为v0的带电粒子,已知重力加速度大小为g.
如图甲所示,小轴正方向水平向右,y轴正方向竖直向上,在xOy平面内有与y轴平行的匀强电场在半径为R的圆形区域加有与xOy平面垂直的匀强磁场,在坐标原点O处放置一带电微粒发射装置.它可以连续不断地发射具有相同质量m、电荷量q(q>0)和初速为v0的带电粒子,已知重力加速度大小为g.(1)当带电微粒发射装置连续不断地沿y轴正方向发射这种带电微粒时,这些带电微粒将沿圆形磁场区域的水平直径方向离开磁场,并继续沿x轴正方向运动.求电场强度和磁感应强度的大小和方向.
(2)调节坐标原点处的带电微粒发射装置,使其在xoy平面内不断地以相同速率v0沿不同方向将这种带电微粒射入第1象限,如图乙所示.现要求这些带电微粒最终都能平行于x轴正方向运动,则在保证匀强电场、匀强磁场的强度及方向不变的条件下,应如何改变匀强磁场的分布区域?并求出符合条件的磁场区域的最小面积.
分析 (1)根据带电微粒所受重力与电场力平衡求出电场强度的大小与方向;由几何关系确定粒子做圆周运动的半径,然后根据半径公式求出磁感应强度;
(2)为使这些带电微粒经磁场偏转后沿x轴正方向运动.由图可知,它们必须从经O点作圆运动的各圆的最高点飞离磁场,结合数学知识求出符合条件的磁场区域的圆方程,最后求出最小面积.
解答 解:(1)带电粒子从坐标原点O处沿y轴正方向进入磁场后,最终沿圆形磁场区域的水平直径离开磁场并继续沿x轴正方向运动,
则带电微粒所受重力与电场力平衡.设电场强度大小为E,由平衡条件得:mg=qE,
解得:E=$\frac{mg}{q}$,电场方向沿y轴正方向;
带电微粒进入磁场后,做匀速圆周运动,且圆运动半径r=R.
设匀强磁场的磁感应强度大小为B.由牛顿第二定律得:
qv0B=m$\frac{{v}_{0}^{2}}{R}$,
解得:B=$\frac{m{v}_{0}}{qR}$,磁场方向垂直于纸面向外.
(2)设由带电微粒发射装置射入第Ⅰ象限的带电微粒的初速度方向与x轴承夹角θ,
则θ满足0≤θ<$\frac{π}{2}$,由于带电微粒最终将沿x轴正方向运动,
故B应垂直于xoy平面向外,带电微粒在磁场内做半径为$\frac{m{v}_{0}}{qB}$匀速圆周运动.
由于带电微粒的入射方向不同,若磁场充满纸面,
它们所对应的运动的轨迹如图所示
为使这些带电微粒经磁场偏转后沿x轴正方向运动.
由图可知,它们必须从经O点作圆运动的各圆的最高点飞离磁场.
这样磁场边界上P点的坐标P(x,y)应满足方程:
x=Rsinθ,
y=R(1-cosθ),
所以磁场边界的方程为:
x2+(y-R)2+R2
由题中0≤θ<$\frac{π}{2}$的条件可知
以θ→$\frac{π}{2}$的角度射入磁场区域的微粒的运动轨迹
(x-R)2+y2=R2
即为所求磁场的另一侧的边界.
因此,符合题目要求的最小磁场的范围应是圆
x2+(y-R)2=R2与圆(x-R)2+y2=R2的
交集部分(图中阴影部分).
由几何关系,可以求得符合条件的磁场的最小面积为:
Smin=($\frac{π}{2}$-1)$\frac{{m}^{2}{v}_{0}^{2}}{{q}^{2}{B}^{2}}$=($\frac{π}{2}$-1)R2.
答:(1)电场强度的大小为$\frac{mg}{q}$方向沿y轴正方向;磁感应强度的大小为$\frac{m{v}_{0}}{qR}$,方向垂直纸面向外.
(2)匀强磁场的分布区域如图所示,求出符合条件的磁场区域的最小面积为($\frac{π}{2}$-1)R2.
点评 本题的关键与难点是由数学知识求满足条件的磁场区域与最小面积,平时要注重数学方法在物理中的应用,该题型常常作为压轴题出现.


| A. | 汽车在OA段运动得最快 | |
| B. | 汽车在AB段静止 | |
| C. | CD段表示汽车的运动方向与初始运动方向相反 | |
| D. | 4 h内汽车的位移大小为零 |
| A. | 感生电场由变化的磁场产生 | |
| B. | 恒定的磁场也能在周围空间产生感生电场 | |
| C. | 感生电场的方向也同样可以用楞次定律和右手螺旋定则来判定 | |
| D. | 感生电场的电场线是闭合曲线,其方向一定是沿逆时针方向 |
 如图所示.质量为m的带正电的小球能沿竖直下滑,磁感应强度为B的匀强磁场方向垂直纸面向外,并与小球运动方向垂直.若d\球电荷量为q.球与墙间的动摩擦因数为μ,求小球下滑的最大速度和最大加速度.
如图所示.质量为m的带正电的小球能沿竖直下滑,磁感应强度为B的匀强磁场方向垂直纸面向外,并与小球运动方向垂直.若d\球电荷量为q.球与墙间的动摩擦因数为μ,求小球下滑的最大速度和最大加速度. 如图甲所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°.在第Ⅲ象限垂直于桌面放置两块相互平行的平板C1、C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m.在第Ⅳ象限垂直于x 轴放置一块平行y轴且沿y轴负向足够长的竖直平板C3,平板C3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m.现将一带负电的小球从桌面上的P点以初速度v0=4$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔,进入磁场区域.已知小球可视为质点,小球的比荷$\frac{q}{m}$=20C/kg,P点与小孔M在垂直于电场方向上的距离为s=$\frac{{\sqrt{2}}}{10}$m,不考虑空气阻力.求:
如图甲所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°.在第Ⅲ象限垂直于桌面放置两块相互平行的平板C1、C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其左端紧贴桌面有一小孔M,小孔M离坐标原点O的距离为L=0.72m.在第Ⅳ象限垂直于x 轴放置一块平行y轴且沿y轴负向足够长的竖直平板C3,平板C3在x轴上垂足为Q,垂足Q与原点O相距d2=0.18m.现将一带负电的小球从桌面上的P点以初速度v0=4$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔,进入磁场区域.已知小球可视为质点,小球的比荷$\frac{q}{m}$=20C/kg,P点与小孔M在垂直于电场方向上的距离为s=$\frac{{\sqrt{2}}}{10}$m,不考虑空气阻力.求:
 如图所示,在xOy坐标系中,x轴上方有方向沿x轴正向的匀强电场,下方有一半径为R的圆形有界匀强磁场,圆心在y轴上,且圆与x轴相切,磁场方向垂直于纸面向外,一质量为m、电荷量为q的带电粒子在坐标为($\frac{7}{4}L$,$\frac{{\sqrt{7}}}{2}L$)的A点,以初速度$\frac{v_0}{2}$沿y轴负方向射入电场,且刚好从O点射入磁场,经磁场偏转后刚好平行于x轴从磁场中射出,不计粒子重力.(结果里可以有根号)
如图所示,在xOy坐标系中,x轴上方有方向沿x轴正向的匀强电场,下方有一半径为R的圆形有界匀强磁场,圆心在y轴上,且圆与x轴相切,磁场方向垂直于纸面向外,一质量为m、电荷量为q的带电粒子在坐标为($\frac{7}{4}L$,$\frac{{\sqrt{7}}}{2}L$)的A点,以初速度$\frac{v_0}{2}$沿y轴负方向射入电场,且刚好从O点射入磁场,经磁场偏转后刚好平行于x轴从磁场中射出,不计粒子重力.(结果里可以有根号)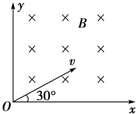 如图所示,在第Ⅰ象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速率沿与x轴成30°角的方向从原点射入磁场,则正、负电子在磁场中运动的时间之比为?
如图所示,在第Ⅰ象限内有垂直纸面向里的匀强磁场,一对正、负电子分别以相同速率沿与x轴成30°角的方向从原点射入磁场,则正、负电子在磁场中运动的时间之比为?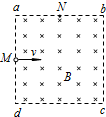 如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中有一匀强磁场,磁感应强度B的方向垂直于纸面向里,一个氢核从ad边的中点M沿着纸面垂直于ad边,以一定的速度射入磁场,正好从ab边中点N射出,现将磁场的磁感应强度变为原来的一半,其他条件不变,则这个氢核射出磁场的位置是( )