题目内容
14.图1是“研究平抛物体运动”的实验装置图,通过描点画出平抛小球的运动轨迹.(1)以下是实验过程中的一些做法,其中合理的有ac.
a.安装斜槽轨道,使其末端保持水平
b.每次小球释放的初始位置可以任意选择
c.每次小球应从同一高度由静止释放
d.为描出小球的运动轨迹,描绘的点可以用折线连接

(2)图2是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取三点A、B、C,测得A、B两点竖直坐标y1为5.0cm、y2为45.0cm,A、B两点水平间距△x为40.0cm.则平抛小球的初速度v0为2.0m/s,若C点的竖直坐标y3为60.0cm,则小球在C点的速度vC为4.0m/s(结果保留两位有效数字,g取10m/s2).
分析 (1)根据实验的原理以及操作中的注意事项确定正确的操作步骤;
(2)根据位移时间公式分别求出抛出点到A点、B点的时间,结合水平位移和时间求出初速度,根据速度位移公式求出C点的竖直分速度,结合平行四边形定则求出C点的速度.
解答 解:(1)a、为了保证小球的初速度水平,安装斜槽轨道时,使其末端水平,故a正确.
b、为了保证小球的初速度相等,每次让小球从斜槽的同一位置由静止释放,故b错误,c正确.
d、描写小球的运动轨迹,描绘的点可以用平滑曲线连接,故d错误.
故选:ac.
(2)根据${y}_{1}=\frac{1}{2}g{{t}_{1}}^{2}$得,${t}_{1}=\sqrt{\frac{2{y}_{1}}{g}}=\sqrt{\frac{2×0.05}{10}}s=0.1s$,根据${y}_{2}=\frac{1}{2}g{{t}_{2}}^{2}$得,${t}_{2}=\sqrt{\frac{2{y}_{2}}{g}}=\sqrt{\frac{2×0.45}{10}}s=0.3s$,则小球的初速度${v}_{0}=\frac{△x}{{t}_{2}-{t}_{1}}=\frac{0.4}{0.3-0.1}m/s=2.0m/s$,c点的竖直分速度${v}_{yc}=\sqrt{2g{y}_{3}}=\sqrt{2×10×0.60}$=$2\sqrt{3}$m/s,根据平行四边形定则知,c点的速度${v}_{c}=\sqrt{{{v}_{0}}^{2}+{{v}_{yc}}^{2}}=\sqrt{4+12}$m/s=4.0m/s.
故答案为:(1)ac (2)c (3)2.0 4.0
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论进行求解,难度不大.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| A. | 多普勒效应是由于波的干涉引起的 | |
| B. | 多普勒效应说明波源的频率发生改变 | |
| C. | 多普勒效应是由于波源与观察者之间有相对运动而产生的 | |
| D. | 只有声波可以产生多普勒效应 |
 如图所示,两个竖直放置的$\frac{3}{4}$圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )
如图所示,两个竖直放置的$\frac{3}{4}$圆弧轨道固定在同一水平地面上,半径R相同,左侧轨道由金属凹槽制成,右侧轨道由金属圆管制成,均可视为光滑.在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别为hA和hB,下列说法正确的是( )| A. | 若使小球A沿轨道运动并且从最高点飞出,释放的最小高度为2R | |
| B. | 若使小球B沿轨道运动并且从最高点飞出,释放的最小高度为$\frac{5}{2}$R | |
| C. | 适当调整hA,可使A球从轨道最高点飞出后,恰好落在轨道右端口处 | |
| D. | 适当调整hB,可使B球从轨道最高点飞出后,恰好落在轨道右端口处 |
| A. | 重心、合力和分力、总电阻、磁感应强度都体现了等效替换的思想 | |
| B. | 质点和点电荷是两种不同的物理方法 | |
| C. | 伽利略用小球在斜面上的运动验证了速度与位移成正比 | |
| D. | 电场强度E=$\frac{F}{q}$、电势φ=$\frac{{E}_{p}}{q}$、电容C=$\frac{Q}{U}$都是采用比值法定义的物理量 |
 质量m=2kg的长木板A放在光滑的水平面上,另一质量m=2kg的物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化的情况如图所示,重力加速度g=10m/s2,则下列说法正确的是( )
质量m=2kg的长木板A放在光滑的水平面上,另一质量m=2kg的物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化的情况如图所示,重力加速度g=10m/s2,则下列说法正确的是( )| A. | 木板A获得的动能为2 J | B. | 系统损失的机械能为1 J | ||
| C. | 木板A的最小长度为1.5 m | D. | A、B间的动摩擦因数为0.1 |
 如图,矩形ABCD为一水平放置的玻璃砖(放在空气中)的截面,在截面所在平面内有一细束激光照射玻璃砖,入射点距底面的高度为h,反射光线和折射光线与底面所在平面的交点到AB的距离分别为l1和l2.在截面所在平面内,改变激光束在AB面上入射点的高度和入射角的大小,当折射光线与底面的交点到AB的距离为l3时,光线恰好不能从底面射出.(已知光在空气中的传播速度为c),求:
如图,矩形ABCD为一水平放置的玻璃砖(放在空气中)的截面,在截面所在平面内有一细束激光照射玻璃砖,入射点距底面的高度为h,反射光线和折射光线与底面所在平面的交点到AB的距离分别为l1和l2.在截面所在平面内,改变激光束在AB面上入射点的高度和入射角的大小,当折射光线与底面的交点到AB的距离为l3时,光线恰好不能从底面射出.(已知光在空气中的传播速度为c),求: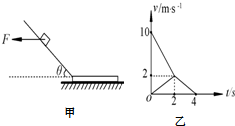 如图甲所示,有一倾角为θ=30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,斜面与木板平滑连接,滑块经过斜面与木板交界处的动能损失可忽略不计.开始时,质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,现将水平力F变为水平向右且大小不变,当滑块滑到木板上时撤去力F,此后滑块和木板在水平面上运动的v-t图象如图乙所示,g取10m/s2.求:
如图甲所示,有一倾角为θ=30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,斜面与木板平滑连接,滑块经过斜面与木板交界处的动能损失可忽略不计.开始时,质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,现将水平力F变为水平向右且大小不变,当滑块滑到木板上时撤去力F,此后滑块和木板在水平面上运动的v-t图象如图乙所示,g取10m/s2.求: