��Ŀ����
7�� ��ͼ��ʾ����ֱ������ϵoxy�У���һ����ͼʾ����������ֱ���ϵ���ǿ�糡�����������д�ֱ��oxyƽ���������ǿ�ų���A�������Ϊ��0��L����C�������Ϊ��2L��0��������������Ϊm���������Ϊq�ĸ�����a��b���ֱ��A���Բ�ͬ���ٶ�����ˮƽ������ٶȴ�С�ֱ�Ϊva=v0��vb=$\sqrt{2}$v0��b���Ӿ����糡ֱ���˶���C�㣬a���ӽ���ų�����˶���C�㣮���������Ӽ������ã��������ӵ���������
��ͼ��ʾ����ֱ������ϵoxy�У���һ����ͼʾ����������ֱ���ϵ���ǿ�糡�����������д�ֱ��oxyƽ���������ǿ�ų���A�������Ϊ��0��L����C�������Ϊ��2L��0��������������Ϊm���������Ϊq�ĸ�����a��b���ֱ��A���Բ�ͬ���ٶ�����ˮƽ������ٶȴ�С�ֱ�Ϊva=v0��vb=$\sqrt{2}$v0��b���Ӿ����糡ֱ���˶���C�㣬a���ӽ���ų�����˶���C�㣮���������Ӽ������ã��������ӵ�����������1��b���Ӿ���C��ʱ���ٶȣ�
��2����ǿ�糡�ĵ糡ǿ��E�Ĵ�С����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�С��
��3����ʹa��b������ͬʱ����C�㣬�������Ӵ�A���Ⱥ����ʱ��ʱ����Ƕ��٣�
���� ��1��b���Ӵ�A��C����ƽ���˶���Ӧ����ƽ���˶��Ĺ��ɿ���������ӵ���C����ٶȣ�
��2������b�ڵ糡������ƽ���˶���Ӧ����ƽ���˶����ɿ�������糡ǿ�ȣ���������a���˶��켣��Ӧ��ţ�ٵڶ����ɿ�������Ÿ�Ӧǿ�ȣ�
��3���ֱ��������a��b���˶�ʱ�䣬Ȼ�����ʱ��
��� �⣺��1��b�����ڵ糡�д�A��C�㣬����ƽ���˶���
2L=$\sqrt{2}$v0tb ��L=$\frac{{v}_{by}}{2}$tb ��
����C��ʱ���ٶȴ�С��vbc=$\sqrt{��\sqrt{2}{v}_{0}��^{2}+{v}_{by}^{2}}$����ã�vbc=2v0 ��
������ˮƽ�ɦȣ�tan��=$\frac{{v}_{by}}{{v}_{0}}$=1����=45�� ��
��2��b�����ڵ糡�д�A��C������ƽ���˶���
qE=ma ��L=$\frac{1}{2}$atb2 ��
�٢ݢ�����ã�E=$\frac{m{v}_{0}^{2}}{qL}$ ��
��a���ӣ��ڵ糡�У�ͬ��������Ӧ����AC���е�D��
��D��ʱ���ٶȴ�СΪ��vaD=$\sqrt{2}$v0����������ˮƽ��45�� ��
a���ӹ�D�����ų�ǰ������ֱ���˶�����F�����ų���������Բ���˶����켣��ͼ��ʾ��Բ�Ľ�Ϊ90�㣩��
��Բ�뾶ΪRa����ţ�ٵڶ����ɵã�qvaDB=m$\frac{{v}_{aD}^{2}}{{R}_{a}}$ ��
�ɼ��ι�ϵ��Ra=$\frac{\sqrt{2}}{4}$L ���ã�B=$\frac{4m{v}_{0}}{qL}$ ��11����
��3���ɢٽ�ã�tb=$\frac{\sqrt{2}L}{{v}_{0}}$��
a���Ӵ�A��F��ˮƽ�������٣���ʱ��ta1=$\frac{3L}{2{v}_{0}}$ ��12��
�ڴų�����ʱ��ta2=$\frac{T}{4}$=$\frac{2��{R}_{a}}{4{v}_{aD}}$=$\frac{��L}{8{v}_{0}}$ ��13��
ʱ����t=ta1+ta2-tb=$\frac{��12+��-8\sqrt{2}��L}{8{v}_{0}}$��
�𣺣�1��b���Ӿ���C��ʱ���ٶȴ�СΪ2v0��������ˮƽ��45��ǣ�
��2����ǿ�糡�ĵ糡ǿ��E�Ĵ�СΪ$\frac{m{v}_{0}^{2}}{qL}$����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ��$\frac{4m{v}_{0}}{qL}$��
��3����ʹa��b������ͬʱ����C�㣬�������Ӵ�A���Ⱥ����ʱ��ʱ�����$\frac{��12+��-8\sqrt{2}��L}{8{v}_{0}}$��
���� ���������ڸ��ϳ��е��˶����������е��ص㣬Ҳ�Ǹ߿��ıؿ������ݣ����ӵ��˶����̵����������Լ��˶���������ǽ���Ĺؼ�������ƽ���˶��Ĵ��������������õ���ƽ���˶��У������ڴų���������Բ���˶�������ȷ�Ļ����˶��켣�������ݼ��ι�ϵȷ������֮��Ĺ�ϵ��

| A������������R1��0��5����1A�� | D����ֵ����R01����ֵΪ200���� |
| B������������R2��0��200����0.5A�� | E����ֵ����R02����ֵΪ25���� |
| C������������R3��0��1750����0.1A�� | F����ֵ����R03����ֵΪ5���� |

��2�����Ӻõ�·֮��ʵ��С����������²�����
��һ���Ƚ������������Ļ�Ƭ�Ƶ����Ҷˣ����ڵ��������ֵΪ�㣻
�ڶ����պϿ���S������Ƭ�������ƣ�ʹ������������ƫ��
���������ֻ�Ƭ����������Ϊa��b���ѹ���䣩�����ڵ�����R�����ֵʹ������������ʾ��ǡ��Ϊ���̶ȵ�$\frac{1}{2}$��
����ʱ�������ʾ����ͼ����ʾ������������������IJ���ֵRgΪ102.5����
��3��Ϊ�Ϻõ����ʵ�飬������Сʵ����ʵ����Ӧѡ��Ļ����������Ͷ�ֵ����ֱ�ΪA��E�������������ǰ����ĸ����
��4��Ҫ��ʱ�Ѹ�������������װ��3.0V���̵ĵ�ѹ��ʹ�ã���Ӧ����������䴮������������������������ѵ�����ĵ���ֵ��Ϊ897.5����
 ��ͼ��ʾ���̶��Ĺ⻬��б��������һ������Ϊm��Բ����Բ������ֱ���õ����ʵ����϶����������ɵ��¶˹̶���ˮƽ�����ϵ�A�㣬��ʼ����ǡ�ô���ԭ��h������Բ���ɾ�ֹ�ظ˻��£������˵ĵˣ�δ�������棩ʱ�ٶ�ǡ��Ϊ�㣮������˵����ȷ���� ��������
��ͼ��ʾ���̶��Ĺ⻬��б��������һ������Ϊm��Բ����Բ������ֱ���õ����ʵ����϶����������ɵ��¶˹̶���ˮƽ�����ϵ�A�㣬��ʼ����ǡ�ô���ԭ��h������Բ���ɾ�ֹ�ظ˻��£������˵ĵˣ�δ�������棩ʱ�ٶ�ǡ��Ϊ�㣮������˵����ȷ���� ��������| A�� | ��Բ���»��Ĺ����У�Բ�������ɺ͵�����ɵ�ϵͳ��е���غ� | |
| B�� | ��Բ���»��Ĺ����У����������ʱ���ɵĵ���������� | |
| C�� | ��Բ���»��Ĺ����У��������ٴλָ�ԭ��ʱԲ���Ķ������ | |
| D�� | ��Բ���»����˵ĵ�ʱ�����ɵĵ�������Ϊmgh |
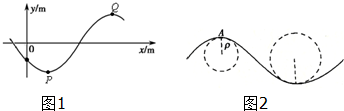
 һ�м�г�Შ��x�ᴫ����t=0ʱ�IJ�����ͼʾ���ʵ�A���ʵ�B���1m��A���ٶ���y��������t=0.02sʱ���ʵ�A�ڶ��ε����������λ�ƴ����ɴ˿�֪��������
һ�м�г�Შ��x�ᴫ����t=0ʱ�IJ�����ͼʾ���ʵ�A���ʵ�B���1m��A���ٶ���y��������t=0.02sʱ���ʵ�A�ڶ��ε����������λ�ƴ����ɴ˿�֪��������| A�� | �˲���x�Ḻ���� | |
| B�� | �˲��Ĵ����ٶ�Ϊ125m/s | |
| C�� | ��t=0ʱ�𣬾���0.04 s���ʵ�A�ز���������Ǩ����5m | |
| D�� | ��t=0.04 sʱ���ʵ�B����ƽ��λ�ã��ٶ���y�Ḻ���� | |
| E�� | ����ò���������ĺᲨ��Ƶ��һ��Ϊ62.5Hz |
| A�� | ��ĸ���˵�����ǺᲨ | |
| B�� | ��Ȼ����ˮ�淴��ʱ������������ⶼ��һ���̶ȵ�ƫ��� | |
| C�� | ������е�Ų���Ƶ��Խ�ߣ������ٶ�ԽС | |
| D�� | �ڲ�ͬ����ϵ�У�����������ز�ͬ����Ĵ����ٶȲ�ͬ |
 ��ͼ��ʾ�������һ������������������̶���ˮƽ�����ϣ��������ҷ��ã������ĺ�����ΪS������ͨ�������쳤������������һ������Ϊm=$\frac{{��}_{0}S}{2g}$��С���壬�������ڶ������ϣ���ʼʱ��������ѹǿ��ͬ����Ϊ����ѹp0��Ϊ��֪����������������¶�ΪT0������ǡ�ô�����ֱ״̬������Ħ�����������ٶ�Ϊg���ֻ��������������¶ȣ���
��ͼ��ʾ�������һ������������������̶���ˮƽ�����ϣ��������ҷ��ã������ĺ�����ΪS������ͨ�������쳤������������һ������Ϊm=$\frac{{��}_{0}S}{2g}$��С���壬�������ڶ������ϣ���ʼʱ��������ѹǿ��ͬ����Ϊ����ѹp0��Ϊ��֪����������������¶�ΪT0������ǡ�ô�����ֱ״̬������Ħ�����������ٶ�Ϊg���ֻ��������������¶ȣ���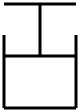 ����Ϊm=2kg����������һ�����ΪS=10cm2�Ŀ�����������Ħ���ƶ��Ļ���������������ΪM=3kg��һ����ϵס������������������һ����𣬴���ƽ��״̬ʱ�������������10cm������ѹǿP0=105Pa��ȡg=10m/s2������������Ĺ����Ϲ�M1=3kg�������ϵͳ����ƽ�⣬����һ�����������������������յ����������������¶Ȳ��䣩
����Ϊm=2kg����������һ�����ΪS=10cm2�Ŀ�����������Ħ���ƶ��Ļ���������������ΪM=3kg��һ����ϵס������������������һ����𣬴���ƽ��״̬ʱ�������������10cm������ѹǿP0=105Pa��ȡg=10m/s2������������Ĺ����Ϲ�M1=3kg�������ϵͳ����ƽ�⣬����һ�����������������������յ����������������¶Ȳ��䣩 �������˽���һ��մ̼�����Ϸ��Ŀ�߿ջ�������Ϸ��ͨ�����������ڻ����£������������������ϴӸߴ����»�ȥ����ͼ��ʾ�����»������е�ijһ�οɿ������뻬��һ���ظ��������»����»����ٶ�Ϊ15m/s���˶θ��µ����Ϊ30�㣬�˺ͻ�����������Ϊ75kg�����������Ĵ�С����f=kv2������vΪ�»��ٶȣ�kΪ���������Ի������¼��Ħ�����������ٶ�ȡ10m/s2����
�������˽���һ��մ̼�����Ϸ��Ŀ�߿ջ�������Ϸ��ͨ�����������ڻ����£������������������ϴӸߴ����»�ȥ����ͼ��ʾ�����»������е�ijһ�οɿ������뻬��һ���ظ��������»����»����ٶ�Ϊ15m/s���˶θ��µ����Ϊ30�㣬�˺ͻ�����������Ϊ75kg�����������Ĵ�С����f=kv2������vΪ�»��ٶȣ�kΪ���������Ի������¼��Ħ�����������ٶ�ȡ10m/s2����