题目内容
4. 如图甲所示,倾角θ=37°的足够长的斜面固定在水平地面上,质量m=1kg的物块在沿斜面向上的恒力F作用下,由斜面底端A处从静止开始沿斜面向上做匀加速运动,物块运动t1=2s时撤去外力F,物块继续向上运动,一段时间后物块到达最高点B.物块运动的v-t图象如图乙所示.取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图甲所示,倾角θ=37°的足够长的斜面固定在水平地面上,质量m=1kg的物块在沿斜面向上的恒力F作用下,由斜面底端A处从静止开始沿斜面向上做匀加速运动,物块运动t1=2s时撤去外力F,物块继续向上运动,一段时间后物块到达最高点B.物块运动的v-t图象如图乙所示.取g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)物块和斜面之间的动摩擦因数;
(2)沿斜面向上的恒力F的大小;
(3)物块从最高点B返回到斜面底端A点所用时间t.
分析 (1)根据图象和加速度公式求出第3s内物块的加速度,再根据牛顿第二定律求出物块和斜面之间的动摩擦因数;
(2)根据图象和加速度公式求出前2s内物块的加速度,再根据牛顿第二定律求出沿斜面向上的恒力F的大小;
(3)根据牛顿第二定律求出当物块从最高点B返回时的加速度,利用图象可得求出AB两点间的距离,然后根据位移时间公式求出物块从最高点B返回到斜面底端A点所用时间t.
解答 解:(1)由物块运动的v-t图象可知,第3s内物块的加速度:
a2=$\frac{△{v}_{2}}{{t}_{2}}$=$\frac{10}{1}$m/s2=10m/s2,
根据牛顿第二定律可得,mgsinθ+μmgcosθ=ma2,
解得:μ=$\frac{{a}_{2}-gsinθ}{gcosθ}$=$\frac{10-10×0.6}{10×0.8}$=0.5,
(2)由物块运动的v-t图象可知,前2s内物块的加速度:
a1=$\frac{△{v}_{1}}{{t}_{1}}$=$\frac{10}{2}$m/s2=5m/s2,
根据牛顿第二定律可得,F-mgsinθ-μmgcosθ=ma1,
代入数据解得:F=15N,
(3)当物块从最高点B返回时,
根据牛顿第二定律可得,mgsinθ-μmgcosθ=ma3,
代入数据解得:a3=2m/s2,
即物块从最高点B返回到斜面底端A点一直做匀加速直线运动,
由图象可得,AB两点间的距离:
x=$\frac{v}{2}$t=$\frac{10}{2}$×3m=15m,
根据位移时间关系,则有:x=$\frac{1}{2}$a3${t}_{3}^{2}$,
解得:t3=$\sqrt{\frac{2x}{{a}_{3}}}$=$\sqrt{\frac{2×15}{2}}$s=$\sqrt{15}$s
答:(1)物块和斜面之间的动摩擦因数为0.5;
(2)沿斜面向上的恒力F的大小为15N;
(3)物块从最高点B返回到斜面底端A点所用时间t为$\sqrt{15}$s.
点评 本题考查学生对牛顿第二定律和匀变速直线运动的位移与时间的关系掌握和应用,关键利用图象求解加速度,再结合牛顿第二定律即可正确解题,难度不大.

 如图电路中,电源电动势、内电阻、R1、R2为定值.闭合S后,将R的滑片向左移动,电压表的示数变化量的绝对值为△U,电阻R2的电压变化量的绝对值为△U′,电源电流变化量的绝对值为△I,下列说法不正确的是( )
如图电路中,电源电动势、内电阻、R1、R2为定值.闭合S后,将R的滑片向左移动,电压表的示数变化量的绝对值为△U,电阻R2的电压变化量的绝对值为△U′,电源电流变化量的绝对值为△I,下列说法不正确的是( )| A. | 通过R1的电流增大,增大量等于$\frac{△U}{{R}_{1}}$ | |
| B. | 通过R2的电流减小,减小量△I大于$\frac{△U}{{R}_{2}}$ | |
| C. | △U′与△I的比值保持不变 | |
| D. | △U与△I的比值保持不变 |
 如图所示电路中,电源电动势为E、内阻为r,电阻R2、R3为定值电阻,R1为滑动变阻器,A、B为电容器的两个极板.当滑动变阻器R1处于某位置时,A、B两板间的带电油滴静止不动.则下列说法中正确的是( )
如图所示电路中,电源电动势为E、内阻为r,电阻R2、R3为定值电阻,R1为滑动变阻器,A、B为电容器的两个极板.当滑动变阻器R1处于某位置时,A、B两板间的带电油滴静止不动.则下列说法中正确的是( )| A. | 仅把R1的触头向右滑动时,电流表读数减小,油滴向下运动 | |
| B. | 仅把R1的触头向右滑动时,电流表读数减小,油滴向上运动 | |
| C. | 仅把两极板A、B间距离减小,油滴向下运动 | |
| D. | 仅把两极板A、B间相对面积减小,油滴向下运动 |
| A. | 石块下落到地面的总时间 | B. | 石子落地前的瞬时速度 | ||
| C. | 石子下落后在第一秒内通过的位移 | D. | 石块落地前通过最后1m位移的时间 |
| A. | N、m/s、m/s2是导出单位 | |
| B. | 后人为了纪念牛顿,N作为力学中的基本单位 | |
| C. | 在国际单位制中,时间的基本单位可以是s,也可以是h | |
| D. | 在不同的力学单位制中,牛顿第二定律的表达式都是F=ma |
 如图所示,一根对称的V字形玻璃管倒置于竖直平面内,V字形玻璃管所在空间充满着方向竖直向下的匀强电场,场强大小E=1000V/m.一个质量m=10-4kg、带电量q=-2×10-6C的小球(小球直径比玻璃管内直径稍小),从A点由静止开始在管内运动,小球与管壁间的动摩擦因数为μ=0.5.已知AB、BC两管长度均为l=2m,倾角α=37°,且管顶B处有一段很短的光滑圆弧,小球在运动过程中带电量保持不变.g=10m/s2.求:
如图所示,一根对称的V字形玻璃管倒置于竖直平面内,V字形玻璃管所在空间充满着方向竖直向下的匀强电场,场强大小E=1000V/m.一个质量m=10-4kg、带电量q=-2×10-6C的小球(小球直径比玻璃管内直径稍小),从A点由静止开始在管内运动,小球与管壁间的动摩擦因数为μ=0.5.已知AB、BC两管长度均为l=2m,倾角α=37°,且管顶B处有一段很短的光滑圆弧,小球在运动过程中带电量保持不变.g=10m/s2.求: 如图所示,M为理想变压器,电表为理想电表,导线电阻忽略不计,原线圈接稳定的正弦式交流电源.当变阻器滑片P向上移动时,读数发生变化的电表是( )
如图所示,M为理想变压器,电表为理想电表,导线电阻忽略不计,原线圈接稳定的正弦式交流电源.当变阻器滑片P向上移动时,读数发生变化的电表是( )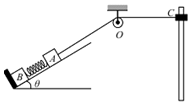 如图所示,质量为m1=20kg的物体A经一轻质弹簧与下方斜面上的质量为m2=20kg的物体B相连,弹簧的劲度系数为 k=50N/m,斜面是光滑的,其倾角为θ=30°.A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体 A,另一端连质量为m3=34kg的物体C.物体C又套在光滑竖直固定 的细杆上,开始时各段绳都处于伸直状态,但没绷紧,OC段绳是水平的,OC段的距离d=6m,A上方的一段绳沿斜面方向.现在静止释放物体C,已知它恰好能使B离开挡板但不继续上升.(结果保留一位有效数字)
如图所示,质量为m1=20kg的物体A经一轻质弹簧与下方斜面上的质量为m2=20kg的物体B相连,弹簧的劲度系数为 k=50N/m,斜面是光滑的,其倾角为θ=30°.A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体 A,另一端连质量为m3=34kg的物体C.物体C又套在光滑竖直固定 的细杆上,开始时各段绳都处于伸直状态,但没绷紧,OC段绳是水平的,OC段的距离d=6m,A上方的一段绳沿斜面方向.现在静止释放物体C,已知它恰好能使B离开挡板但不继续上升.(结果保留一位有效数字)