题目内容
6. 如图所示,一质量为m=1kg的物块(可视为质点)从倾角为37°的斜面顶点A由静止开始在沿斜面向下的恒力F=50N的作用下运动一段距离后撤去该力,此后物块继续沿轨道ABC到达平台上C点时(BC水平,物块经过B点时无能量损失)以v0=$\sqrt{3}$m/s的速度水平抛出.当物块运动到水平面上的D点时,恰好沿切线方向进入光滑圆弧轨道DEF.已知H=1.65m,h=0.45m,s=1.5m,R=0.5m,物块与轨道ABC间的动摩擦因数为μ=0.5,g取10m/s2.
如图所示,一质量为m=1kg的物块(可视为质点)从倾角为37°的斜面顶点A由静止开始在沿斜面向下的恒力F=50N的作用下运动一段距离后撤去该力,此后物块继续沿轨道ABC到达平台上C点时(BC水平,物块经过B点时无能量损失)以v0=$\sqrt{3}$m/s的速度水平抛出.当物块运动到水平面上的D点时,恰好沿切线方向进入光滑圆弧轨道DEF.已知H=1.65m,h=0.45m,s=1.5m,R=0.5m,物块与轨道ABC间的动摩擦因数为μ=0.5,g取10m/s2.(1)求物块运动到D点的速度是多少?
(2)求物块运动到E点时,对圆弧轨道的压力;
(3)求撤去力F时物块运动的位移大小.
分析 (1)物体离开C做平抛运动,由自由落体运动的规律求出物体落在D时的竖直分速度,然后应用运动的合成与分解求出平抛运动的初速度大小,即物块运动到D点的速度.
(2)通过计算分析清楚物体的运动过程,由机械能能守恒定律求出物体在E点的速度,然后又牛顿运动定律求出物体对圆弧轨道压力大小.
(3)对物块从A运动到C的过程,由动能定理即可求解.
解答 解:(1)物体从C点抛出后竖直方向做自由落体运动,到D点时,竖直方向分速度:vy=$\sqrt{2gh}$=$\sqrt{2×10×0.45}$m/s=3m/s
则小球运动到D点的速度为:
vD=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{3+9}$=2$\sqrt{3}$m/s
(2)由(1)得vD与水平方向成60°,DE间的高度差为 h=R(1-cos60°)=0.5×$\frac{1}{2}$m=0.25m
由D到E,根据机械能守恒定律得:
$\frac{1}{2}$mvE2=$\frac{1}{2}$mvD2+mgh
代入数据得:vE=$\sqrt{17}$m/s
在E点,根据向心力公式得:FN-mg=m$\frac{{v}_{E}^{2}}{R}$
解得:FN=10+1×$\frac{17}{0.5}$=44N
根据牛顿第三定律可知,小球运动到E点时,对圆弧轨道的压力为44N.
(3)由A到C运用动能定理得:
FS+mghAC-μmgcos37°•xAB-μmg•s=$\frac{1}{2}$mvC2-0
代入数据得:50S+10×1.2-0.5×10×0.8-0.5×10×1.5=$\frac{1}{2}×1×3$
解得 S=0.01m
答:
(1)物块运动到D点的速度是2$\sqrt{3}$m/s.
(2)物块运动到E点时,对圆弧轨道的压力是44N;
(3)撤去力F时物块运动的位移大小是0.01m.
点评 本题主要考查了平抛运动、向心力公式、动能定理的直接应用,要求同学们能正确对物体进行受力分析,灵活选取相应的物理规律.

 学习实践园地系列答案
学习实践园地系列答案| A. | 布朗运动就是分子的无规则运动 | |
| B. | 布朗运动和扩散现象都反映了分子的热运动 | |
| C. | 水中撒一点胡椒粉,加热时发现水中的胡椒粉在翻滚,这说明温度越高,布朗运动越激烈 | |
| D. | 温度越高,则扩散现象越明显 |
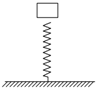 如图所示,地面上竖直放一根轻弹簧,其下端和地面连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )
如图所示,地面上竖直放一根轻弹簧,其下端和地面连接,一物体从弹簧正上方距弹簧一定高度处自由下落,则( )| A. | 物体和弹簧接触时,物体的动能最大 | |
| B. | 物体在反弹阶段,动能一直增加,直到物体脱离弹簧为止 | |
| C. | 与弹簧接触的整个过程,物体的动能与重力势能之和先增大后减小 | |
| D. | 与弹簧接触的整个过程,物体的动能与弹簧弹性势能之和先增大后减小 |
| A. | 据公式I=$\frac{P}{U}$,提高电压后输电线上的电流降为原来的$\frac{1}{20}$ | |
| B. | 据公式I=$\frac{U}{R}$,提高电压后输电线上的电流增为原来的20倍 | |
| C. | 据公式P=I2R,提高电压后输电线上的功率损耗减为原来的$\frac{1}{400}$ | |
| D. | 据公式P=$\frac{{U}^{2}}{R}$,提高电压后输电线上的功率损耗将增大为原来400倍 |
 如图1所示,放在斜面上的物体静止,若加入一个垂直斜面的外力F作用物体上,物体仍静止(如图2).动摩擦因数μ,物体质量m,斜面倾角θ,则( )
如图1所示,放在斜面上的物体静止,若加入一个垂直斜面的外力F作用物体上,物体仍静止(如图2).动摩擦因数μ,物体质量m,斜面倾角θ,则( )| A. | 物体受到的摩擦力一定是μmgcosθ | |
| B. | 一定有μ≥tanθ | |
| C. | 物体可能受三个力作用,也可能受四个力作用 | |
| D. | 物体一定受四个力作用 |

| A. | 沿y轴方向做匀速运动 | B. | 沿x轴方向做匀速运动 | ||
| C. | 沿y轴方向做匀加速运动 | D. | 沿x轴方向做匀加速运动 |
 如图所示的系统,绳子的质量忽略不计且绳子不可以伸长,滑轮和绳子的摩擦力忽略不计,求M1的加速度.
如图所示的系统,绳子的质量忽略不计且绳子不可以伸长,滑轮和绳子的摩擦力忽略不计,求M1的加速度. 如图所示,一轻弹簧直立地面上,其劲度系数为400N/m,弹簧上端与盒子A连接在一起,盒子内装物体B,B的上下表面恰与盒子接触,A和B的质量mA=mB=1.0kg,g=10m/s2,不计空气阻力.先将A向上抬高使弹簧伸长5.0cm后,从静止释放,释放后A和B一起做简谐运动.试求:
如图所示,一轻弹簧直立地面上,其劲度系数为400N/m,弹簧上端与盒子A连接在一起,盒子内装物体B,B的上下表面恰与盒子接触,A和B的质量mA=mB=1.0kg,g=10m/s2,不计空气阻力.先将A向上抬高使弹簧伸长5.0cm后,从静止释放,释放后A和B一起做简谐运动.试求: