��Ŀ����
18��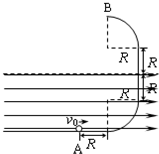 ��ͼ��ʾ������ֱƽ���ڣ�����$\frac{1}{4}$Բ����ֱ�����ϳɹ⻬��Ե������ڸ߶�h=2R���´���E=$\frac{mg}{q}$������ˮƽ���ҵ���ǿ�糡���������γߴ���ͼ��ʾ��һ������Ϊq������Ϊm�Ĵ������С���A���Գ��ٶ�v0�����˶���
��ͼ��ʾ������ֱƽ���ڣ�����$\frac{1}{4}$Բ����ֱ�����ϳɹ⻬��Ե������ڸ߶�h=2R���´���E=$\frac{mg}{q}$������ˮƽ���ҵ���ǿ�糡���������γߴ���ͼ��ʾ��һ������Ϊq������Ϊm�Ĵ������С���A���Գ��ٶ�v0�����˶�����1����С��ʼ���ع���ڲ��˶��������룬��v0�Ĵ�СӦ����ʲô������
��2����v0ȡ��1���е��ٽ�ֵʱ��������С����������
��3����С���˶�����ߵ�Bʱ�Թ����ѹ������mg������С���B�����ˮƽ��������е糡�������Ĺ���
���� С�������˶�ֻ�������ڹ�����˶��������룬ĩ�ٶȿ���Ϊ�㣬���ݹ��ܹ�ϵ�з��� $\frac{1}{2}m{v}_{0}^{2}+qE2R-mg3R��0$���ɣ�
�������͵糡���ϳɺ���һ��ȫ�µij������ҵ���Ч������͵㣬��ʹ�С��Թ���ĵ�������ݶ��ܶ���$qE•��1+\frac{\sqrt{2}}{2}��R-mg•��1-\frac{\sqrt{2}}{2}��R=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$����������Ч������͵㴦���ٶȣ��ٸ��ݺ����ṩ������������ѹ����
���ݺ����ṩ���������С��ͨ��B����ٶȣ�����B���С������ֱ�����������������˶���С���B���䵽�糡�Ϸ�ˮƽ����������������ֱ���˶���С�����糡�У���ˮƽ�����ϣ��ܵ�ˮƽ���ҵ糡����ˮƽ�������ȼ����˶���������ֱ������˶�����ʱ�䣬��ˮƽ�����Ϸֶμ���λ�ƣ�����qEx����糡���������
��� �⣺��1�����պò�����������qE•2R-mg•4R=$\frac{1}{2}m��\sqrt{gR}��^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
��ã�${v}_{0}=\sqrt{2gR}$������Ӧ�У�${v}_{0}��\sqrt{2gR}$
��2��������糡���ĺ���F=$\sqrt{2}mg$��������ˮƽ�����450��б����
�������±�1/4Բ���е㣨��ΪC�������������$qE•��1+\frac{\sqrt{2}}{2}��R-mg•��1-\frac{\sqrt{2}}{2}��R=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$
N-F=$\frac{m{v}_{c}^{2}}{R}$ ����N-qEcos45��-mgsin45��=$\frac{m{v}_{c}^{2}}{R}$ ��
��ã�$N=��2+3\sqrt{2}��mg$
��3������ߵ�B��mg+${N}_{B}=\frac{m{v}_{B}^{2}}{R}$
��ã�${v}_{B}=\sqrt{2gR}$
��B����糡��ʱ�䣺${t}_{1}=\sqrt{\frac{4R}{g}}$
��B����ˮƽ�����ʱ�䣺${t}_{2}=\sqrt{\frac{8R}{g}}$
���ԣ��ڸ��ϳ��е��˶�ʱ�䣺$��t={t}_{2}-{t}_{1}=2��\sqrt{2}-1��\sqrt{\frac{R}{g}}$
ˮƽ����${a}_{x}=\frac{qE}{m}=g$
$��x={v}_{B}•��t-\frac{1}{2}{a}_{x}����t��^{2}=2��\sqrt{2}-1��R$����������
B�㵽���ˮƽ������̵糡��������$W=-qE•��x=-2��\sqrt{2}-1��mgR$
�𣺣�1����С�������˶�ֻ�������ڹ�����˶��������룬��С��v0Ӧ����${v}_{0}��\sqrt{2gR}$��
��2��v0Ϊ���ֵʱ����С��Թ���������Ϊ$��2+3\sqrt{2}��mg$
��3��С���B�����ˮƽ��������е糡�������Ĺ�Ϊ$2��\sqrt{2}-1��mgR$��
���� ����Ҫ�ܽ������͵糡���ϳɺ���һ��ȫ�µij������ҵ���Ч������͵㣬���ݶ��ܶ�����ţ�ٵڶ����������ʽ��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ���ٶ�Խ���������˶����ٶ�ҲԽ�� | |
| B�� | ���ٶȴ������϶����������˶� | |
| C�� | �����ٶ���ʱ��������ܳ����˶������ٶ����� | |
| D�� | �����ٶȼ�Сʱ��������˶��ٶ��Կ��������� |
 ��������ֱ�Ϊq1��q2�ĵ��ɷ���x���ϵ�O��M���㣬����������ϸ�����Ʀ���x�仯�Ĺ�ϵ��ͼ��ʾ������A��N����ĵ���Ϊ�㣬ND����C�������ߣ�������˵������ȷ���ǣ�������
��������ֱ�Ϊq1��q2�ĵ��ɷ���x���ϵ�O��M���㣬����������ϸ�����Ʀ���x�仯�Ĺ�ϵ��ͼ��ʾ������A��N����ĵ���Ϊ�㣬ND����C�������ߣ�������˵������ȷ���ǣ�������| A�� | |q1|��|q2| | |
| B�� | q1�����磬q2������ | |
| C�� | C��ĵ糡ǿ�ȴ�СΪ�� | |
| D�� | ��һ�����ɴ�N���Ƶ�D�㣬�糡������������������ |
| A�� | �������������������˹� | B�� | һ���Ǻ��������������˹� | ||
| C�� | һ�����������������˹� | D�� | ������Ħ�������������˹� |
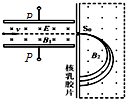 1922��Ӣ������ѧ�Ұ�˹���������ǵķ�����ͬλ�غ������ǵ��о��ٻ���ŵ������ѧ������һ�����ӣ�������������������������Ǻ���˶��켣��ͼ��ʾ��������˵����ȷ���ǣ�������
1922��Ӣ������ѧ�Ұ�˹���������ǵķ�����ͬλ�غ������ǵ��о��ٻ���ŵ������ѧ������һ�����ӣ�������������������������Ǻ���˶��켣��ͼ��ʾ��������˵����ȷ���ǣ�������| A�� | �����������Ӵ����� | |
| B�� | �ٶ�ѡ�������ϼ�������� | |
| C�� | �ڴų�B2���˶��뾶Խ������ӣ�����Խ�� | |
| D�� | �ڴų�B2���˶��뾶Խ������ӣ��Ⱥ�q/mԽС |
| A�� | ���ٶ���С�����ٶ������� | |
| B�� | ���ٶ��������ٶ���С | |
| C�� | ���ٶȲ��䣬���ٶ�Ҳ���ı� | |
| D�� | ���ٶȴ�С���䷽��ı䣬���ٶȱ��ֲ��� |
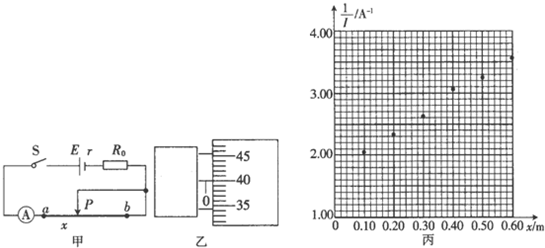
��1��ʵ����������������õ���˿��ֱ����ͼ����ʾ����ʾ��Ϊd=0.400mm��
��2��ʵ��ʱ�պϿ��أ����ڻ�ƬP��λ�ã��ֱ������ÿ��ʵ����aP����x����Ӧ�ĵ���ֵI��ʵ���������±���ʾ��
| x��m�� | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| I��A�� | 0.49 | 0.43 | 0.38 | 0.33 | 0.31 | 0.38 |
| $\frac{l}{I}$��A-1�� | 2.02 | 2.33 | 2.63 | 3.03 | 3.23 | 3.57 |
�ڸ���ͼ����$\frac{l}{I}$-x��ϵͼ������ؾ���������壬����õ�Դ������Ϊ1.4����������λ��Ч���֣���
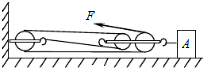 ��ͼ��ʾ����������������A��ˮƽ����������ֱ���˶�����֪mA=500kg��F=612.5N��������Ļ�еЧ�ʦ�=80%��
��ͼ��ʾ����������������A��ˮƽ����������ֱ���˶�����֪mA=500kg��F=612.5N��������Ļ�еЧ�ʦ�=80%��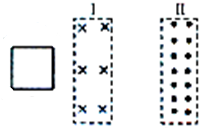 ��ͼ��ʾ����������ǿ�ų�����ΪL���Ÿ�Ӧǿ�Ⱦ�ΪB���������߿�߳�ҲΪL������ΪR�����߿����ٶ�v���ٴ���������ʱ�����������Ĺ��Ƕ��٣�
��ͼ��ʾ����������ǿ�ų�����ΪL���Ÿ�Ӧǿ�Ⱦ�ΪB���������߿�߳�ҲΪL������ΪR�����߿����ٶ�v���ٴ���������ʱ�����������Ĺ��Ƕ��٣�