题目内容
15.为测定一段金属丝的电阻率ρ,某同学设计了如图甲所示的电路.ab是一段电阻率较大的粗细均匀的电阻丝,电路中的保护电阻R0=4.0Ω电源的电动势E=3.0V,电流表内阻忽略不计,滑片P与电阻丝始终接触良好.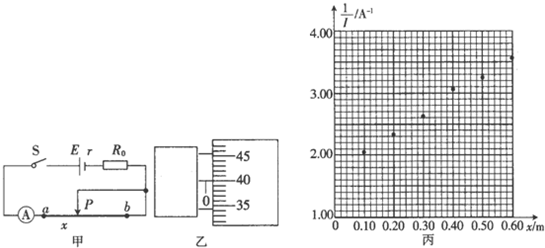
(1)实验中用螺旋测微器测得电阻丝的直径如图乙所示,其示数为d=0.400mm.
(2)实验时闭合开关,调节滑片P的位置,分别测量出每次实验中aP长度x及对应的电流值I,实验数据如下表所示:
| x(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| I(A) | 0.49 | 0.43 | 0.38 | 0.33 | 0.31 | 0.38 |
| $\frac{l}{I}$(A-1) | 2.02 | 2.33 | 2.63 | 3.03 | 3.23 | 3.57 |
②根据图丙中$\frac{l}{I}$-x关系图线纵轴截距的物理意义,可求得电源的内阻为1.4Ω(保留两位有效数字).
分析 (1)螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数.
(2)应用描点法作图作出图象;求出图象的函数表达式,然后根据图象求出电阻率.
解答  解:(1)由图乙所示螺旋测微器可知,其示数为0mm+40.0×0.01mm=0.400mm.
解:(1)由图乙所示螺旋测微器可知,其示数为0mm+40.0×0.01mm=0.400mm.
(2)①如图所示由图丙所示图象由电阻定律可得,R=ρ$\frac{x}{s}$,
由闭合电路欧姆定律,则有,I=$\frac{E}{{R}_{0}+R+r}$,
那么$\frac{1}{I}$=$\frac{r+{R}_{0}}{E}$+$\frac{R}{E}$,
由电阻定律可知:R=ρ$\frac{x}{S}$=ρ$\frac{x}{π(\frac{d}{2})^{2}}$=ρ$\frac{4x}{π{d}^{2}}$,
则:$\frac{1}{I}$=$\frac{r+{R}_{0}}{E}$+$\frac{4ρ}{π{d}^{2}E}$x,
$\frac{1}{I}$-x图象的斜率:k=$\frac{4ρ}{π{d}^{2}E}$,
由图示图象可知:k=$\frac{△\frac{1}{I}}{△x}$=$\frac{3-1.8}{0.42}$≈2.86,
联立解得电阻率为:ρ=$\frac{kEπ{d}^{2}}{4}$
代入数据得:ρ=1.1×10-6Ω•m;
根据图丙中$\frac{l}{I}$-x关系图线纵轴截距为1.8,此时待测电阻丝电阻为零,由闭合电路欧姆定律得:
E=I(r+R0)
即:3=$\frac{1}{1.8}$(r+4.0)
得:r=1.4Ω
故答案为:(1)0.400;(2)$\frac{4ρ}{Eπ{d}^{2}}$,1.1×10-6;1.4Ω.
点评 螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器示数,螺旋测微器需要估读;要掌握应用图象法处理实验数据的方法.

 名校课堂系列答案
名校课堂系列答案| A. | 伏特V | B. | 库仑C | C. | 法拉F | D. | 安培A |

| A. | 只受重力 | B. | 只受重力和支持力 | ||
| C. | 只受重力和摩擦力 | D. | 只受重力、支持力和摩擦力 |
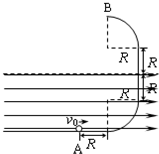
 如图,磁感强度为B的匀强磁场,垂直穿过平面直角坐标系的第I象限.一质量为m的带电量为q的带电粒子以速度V0从O点沿着与y轴夹角为30°方向进入磁场,运动到A点时的速度方向平行于x轴,那么( )
如图,磁感强度为B的匀强磁场,垂直穿过平面直角坐标系的第I象限.一质量为m的带电量为q的带电粒子以速度V0从O点沿着与y轴夹角为30°方向进入磁场,运动到A点时的速度方向平行于x轴,那么( )| A. | 粒子带正电 | B. | 粒子带负电 | ||
| C. | 粒子由O到A经历时间$t=\frac{πm}{3qB}$ | D. | 粒子由O到A经历时间$t=\frac{πm}{6qB}$ |
| A. | 125m,向东 | B. | 25m,向东 | C. | 12.5m,向西 | D. | 25m,向西 |
 如图所示,在竖直平面内,两个$\frac{1}{4}$圆弧与直轨道组合成光滑绝缘轨道,在高度h=2R以下存在E=$\frac{mg}{q}$、方向水平向右的匀强电场,其它几何尺寸如图所示,一带电量为q、质量为m的带正电的小球从A处以初速度v0向右运动.
如图所示,在竖直平面内,两个$\frac{1}{4}$圆弧与直轨道组合成光滑绝缘轨道,在高度h=2R以下存在E=$\frac{mg}{q}$、方向水平向右的匀强电场,其它几何尺寸如图所示,一带电量为q、质量为m的带正电的小球从A处以初速度v0向右运动. 内垫光滑的圆管弯成半径相同的两段弧,放在同一竖直圆内如图所示,$\widehat{ADC}$=$\widehat{ABC}$,一小球以某一初速度v0分别沿$\widehat{ADC}$和$\widehat{ABC}$到达C点所需时间分别为t1和t2,则( )
内垫光滑的圆管弯成半径相同的两段弧,放在同一竖直圆内如图所示,$\widehat{ADC}$=$\widehat{ABC}$,一小球以某一初速度v0分别沿$\widehat{ADC}$和$\widehat{ABC}$到达C点所需时间分别为t1和t2,则( )