题目内容
6. 将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2,下列说法中正确的是( )
将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反.该过程的v-t图象如图所示,g取10m/s2,下列说法中正确的是( )| A. | 小球上升过程与下落过程所用时间之比为2:3 | |
| B. | 小球所受重力和阻力大小之比为5:1 | |
| C. | 小球落回到抛出点的速度大小为8$\sqrt{6}$m/s | |
| D. | 小球下落过程中,受到向上的空气阻力,处于超重状态 |
分析 根据图象可以得到上升过程中的加速度的大小,根据牛顿第二定律可以求得阻力的大小,下降过程的加速度的大小,利用位移时间的关系可以求得运动的时间关系,根据速度和位移公式可求得小球回到抛出点时速度;由加速度的方向分析物体超重还是失重状态.
解答 解:A、根据速度时间图线知,小球向上做匀减速直线运动的加速度大小${a}_{1}=\frac{24}{2}m/{s}^{2}=12m/{s}^{2}$,根据牛顿第二定律得,mg+f=ma1,解得阻力f=ma1-mg=1×12-10N=2N,下降的加速度${a}_{2}=\frac{mg-f}{m}=\frac{10-2}{1}m/{s}^{2}=8m/{s}^{2}$,对上升的过程,采用逆向思维得,$h=\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$,对下降的过程,有:$h=\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$,可知$t=\sqrt{\frac{2h}{a}}$,则所用的时间之比为$\sqrt{2}:\sqrt{3}$,故A错误.
B、重力的大小为10N,阻力为2N,则重力和阻力大小之比为5:1,故B正确.
C、小球上升到最高点的高度h=$\frac{1}{2}×2×24m=24m$,根据速度位移公式得,小球落回抛出点的速度$v=\sqrt{2{a}_{2}h}=\sqrt{2×8×24}$m/s=$8\sqrt{6}$m/s,故C正确.
D、小球在下落的过程中,加速度方向向下,处于失重状态,故D错误.
故选:BC.
点评 本题考查了牛顿第二定律和速度时间图线的运用,知道加速度是联系力学和运动学的桥梁,知道图线的斜率表示加速度,图线与时间轴围成的面积表示位移.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13. 一位同学设计了一个小实验,他将细绳的一端系在手指上,绳印另一端系在直杆的A端,杆的左端垂直顶在掌心上,组成一个“三角支架”,如图所示.在杆的A端悬挂不同重物,并保持静止.下列说法正确的是( )
一位同学设计了一个小实验,他将细绳的一端系在手指上,绳印另一端系在直杆的A端,杆的左端垂直顶在掌心上,组成一个“三角支架”,如图所示.在杆的A端悬挂不同重物,并保持静止.下列说法正确的是( )
 一位同学设计了一个小实验,他将细绳的一端系在手指上,绳印另一端系在直杆的A端,杆的左端垂直顶在掌心上,组成一个“三角支架”,如图所示.在杆的A端悬挂不同重物,并保持静止.下列说法正确的是( )
一位同学设计了一个小实验,他将细绳的一端系在手指上,绳印另一端系在直杆的A端,杆的左端垂直顶在掌心上,组成一个“三角支架”,如图所示.在杆的A端悬挂不同重物,并保持静止.下列说法正确的是( )| A. | 绳子AD有拉伸绳子和压缩杆AC的作用效果 | |
| B. | 绳子AD的拉力小于绳子AB的拉力 | |
| C. | 杆AC受到的压力一定大于绳子AB受到的拉力 | |
| D. | 所挂重物质量越大,绳和杆对手的作用力也越大 |
11. 如图所示,水平传送带AB距离地面的高度为h,以恒定速率v0顺时针运行.甲、乙两滑块(视为质点)之间夹着一个压缩的轻弹簧(长度不计),在AB的正中间位置由静止释放它们时,弹簧立即弹开,两滑块以相同的速率分别向左、右运动.下列判断正确的是( )
如图所示,水平传送带AB距离地面的高度为h,以恒定速率v0顺时针运行.甲、乙两滑块(视为质点)之间夹着一个压缩的轻弹簧(长度不计),在AB的正中间位置由静止释放它们时,弹簧立即弹开,两滑块以相同的速率分别向左、右运动.下列判断正确的是( )
 如图所示,水平传送带AB距离地面的高度为h,以恒定速率v0顺时针运行.甲、乙两滑块(视为质点)之间夹着一个压缩的轻弹簧(长度不计),在AB的正中间位置由静止释放它们时,弹簧立即弹开,两滑块以相同的速率分别向左、右运动.下列判断正确的是( )
如图所示,水平传送带AB距离地面的高度为h,以恒定速率v0顺时针运行.甲、乙两滑块(视为质点)之间夹着一个压缩的轻弹簧(长度不计),在AB的正中间位置由静止释放它们时,弹簧立即弹开,两滑块以相同的速率分别向左、右运动.下列判断正确的是( )| A. | 甲、乙两滑块可能落在传送带的同一侧 | |
| B. | 甲、乙两滑块不可能落在传送带的同一侧 | |
| C. | 甲、乙两滑块可能落在传送带的左右两侧,但距释放点的水平距离一定不相等 | |
| D. | 如果传送带足够长,甲、乙两滑块最终速度一定相等 |
15. 如图所示,物体A、B的质量均为M,物体C的质量为$\frac{1}{4}$M,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,重力加速度为g,系统在由静止释放后的运动过程中,下列说法正确的是( )
如图所示,物体A、B的质量均为M,物体C的质量为$\frac{1}{4}$M,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,重力加速度为g,系统在由静止释放后的运动过程中,下列说法正确的是( )
 如图所示,物体A、B的质量均为M,物体C的质量为$\frac{1}{4}$M,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,重力加速度为g,系统在由静止释放后的运动过程中,下列说法正确的是( )
如图所示,物体A、B的质量均为M,物体C的质量为$\frac{1}{4}$M,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,重力加速度为g,系统在由静止释放后的运动过程中,下列说法正确的是( )| A. | 物体A上升加速度为$\frac{1}{3}$g | B. | 物体A上升加速度为$\frac{1}{9}$g | ||
| C. | 轻绳对A的拉力为Mg | D. | 物体C对B的拉力为$\frac{2}{9}$Mg |
16. 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0-x2段是关于直线x=x1对称的曲线,x2-x3段是直线,则下列说法正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0-x2段是关于直线x=x1对称的曲线,x2-x3段是直线,则下列说法正确的是( )
 一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0-x2段是关于直线x=x1对称的曲线,x2-x3段是直线,则下列说法正确的是( )
一带负电的粒子只在电场力作用下沿x轴正向运动,其电势能Ep随位移x变化的关系如图所示,其中0-x2段是关于直线x=x1对称的曲线,x2-x3段是直线,则下列说法正确的是( )| A. | x1处电场强度最小,但不为零 | |
| B. | x2~x3段电场强度大小方向均不变,为一定值 | |
| C. | 粒子在0~x2段做匀变速运动,x2~x3段做匀速直线运动 | |
| D. | 在0、x1、x2、x3处电势φ0、φ1、φ2、φ3的关系为φ3>φ2=φ0>φ1 |
 某人设计了一种测量物体质量的电子秤,其原理图如图所示,主要由四部分构成:踏板、压力传感器R(实际上是一个阻值可随压力变化的电阻器)、显示体重的仪表G(实质上是电流表)和电源,已知踏板质量为10kg,电流表量程为3A,内阻为1Ω,电源电动势为15V,内阻为1Ω,电阻R随压力F变化的关系式为:R=24-0.01F(F和R的单位分别为N和Ω),求:(g=10m/s2).
某人设计了一种测量物体质量的电子秤,其原理图如图所示,主要由四部分构成:踏板、压力传感器R(实际上是一个阻值可随压力变化的电阻器)、显示体重的仪表G(实质上是电流表)和电源,已知踏板质量为10kg,电流表量程为3A,内阻为1Ω,电源电动势为15V,内阻为1Ω,电阻R随压力F变化的关系式为:R=24-0.01F(F和R的单位分别为N和Ω),求:(g=10m/s2).
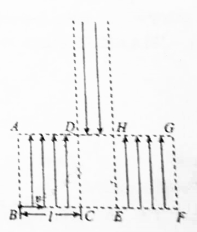 如图所示,两个边长均为l的正方形区城ABCD和EFGH内有竖直向上的匀强电场.DH上方有足够长的竖直向下的匀强电场.一带正电的粒子,质量为m、电荷量为q,以速度v从B点沿BC方向射人匀强电场.已知三个区域内的场强大小相等.且E=$\frac{m{v}^{2}}{ql}$,今在CDHE区域内加上合适的垂直纸面向里的匀强磁场.粒子经过该磁场后恰能从DH的中点竖直向上射人电场,粒子的重力不计,求:
如图所示,两个边长均为l的正方形区城ABCD和EFGH内有竖直向上的匀强电场.DH上方有足够长的竖直向下的匀强电场.一带正电的粒子,质量为m、电荷量为q,以速度v从B点沿BC方向射人匀强电场.已知三个区域内的场强大小相等.且E=$\frac{m{v}^{2}}{ql}$,今在CDHE区域内加上合适的垂直纸面向里的匀强磁场.粒子经过该磁场后恰能从DH的中点竖直向上射人电场,粒子的重力不计,求: 如图所示,一水平的足够长的浅色长传送带与平板紧靠在一起,且上表面在同一水平面.传送带上左端放置一质量为m=1kg的煤块(视为质点),煤块与传送带及煤块与平板上表面之间的动摩擦因数为均为μ1=0.1.初始时,传送带与煤块及平板都是静止的.现让传送带以恒定的向右加速度a=3m/s2开始运动,当其速度达到v=1.5m/s后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动,随后,在平稳滑上右端平板上的同时,在平板右侧施加一个水平恒力F=17N,F作用了0.5s时煤块与平板速度恰相等,此时刻撤去F.最终煤块没有从平板上滑下,已知平板质量M=4kg,(重力加速度为g=10m/s2),求:
如图所示,一水平的足够长的浅色长传送带与平板紧靠在一起,且上表面在同一水平面.传送带上左端放置一质量为m=1kg的煤块(视为质点),煤块与传送带及煤块与平板上表面之间的动摩擦因数为均为μ1=0.1.初始时,传送带与煤块及平板都是静止的.现让传送带以恒定的向右加速度a=3m/s2开始运动,当其速度达到v=1.5m/s后,便以此速度做匀速运动.经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动,随后,在平稳滑上右端平板上的同时,在平板右侧施加一个水平恒力F=17N,F作用了0.5s时煤块与平板速度恰相等,此时刻撤去F.最终煤块没有从平板上滑下,已知平板质量M=4kg,(重力加速度为g=10m/s2),求: