题目内容
20. 如图所示,A、B、C三个小物块放置在光滑水平面上,A紧靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现使物块C获得水平向左的初速度v0,物块C与物块B发生碰撞并粘在一起不再分离.试求:
如图所示,A、B、C三个小物块放置在光滑水平面上,A紧靠在墙壁,A、B之间用轻弹簧连接,它们的质量分别为mA=m,mB=2m,mC=m.现使物块C获得水平向左的初速度v0,物块C与物块B发生碰撞并粘在一起不再分离.试求:(1)物块A离开墙前,弹簧的最大弹性势能Em;
(2)物块A离开墙后,物块C的最小速度vmin.
分析 (1)C、B碰撞过程遵守动量守恒,由动量守恒定律列式求出碰后B、C的共同速度v.再运用机械能守恒求解弹簧的最大弹性势能Em.
(2)在A离开墙壁时,弹簧处于原长,B、C以速度v向右运动,之后,A、B、C及弹簧组成的系统机械能守恒,动量也守恒.由于弹簧的作用,A的速度逐渐增大,BC的速度逐渐减小,当弹簧再次恢复原长时,B与C的速度最小,由动量守恒定律和功能关系即可求出.
解答 解:(1)设物块C与B发生碰撞粘在一起时的速度为v.C、B碰撞过程,选取向左为正方向,根据动量守恒定律得:
mcv0=(mc+mB)v
得:v=$\frac{1}{3}$v0.
当C与B一起压缩弹簧至速度为零时弹簧的弹性势能最大.以B、C和弹簧组成的系统为研究对象,根据机械能守恒定律有:
Em=$\frac{1}{2}$(mc+mB)2.
联立以上两式解得:Em=$\frac{1}{6}m{v}_{0}^{2}$.
(2)在A离开墙壁时,弹簧第一次恢复原长,B、C以速度v向右运动;
在A离开墙壁后,由于弹簧的作用,A的速度逐渐增大,B、C的速度逐渐减小,当弹簧再次恢复原长时,B与C的速度最小.设B与C的速度最小时A的速度为vA.
选取向右为正方向,由A、B、C三物体组成系统动量守恒得:
(mB+mC)v=mAvA+(mB+mC)vmin
又由能量守恒定律有:$\frac{1}{2}$(mB+mC)v2=$\frac{1}{2}$mAvA2+$\frac{1}{2}$(mB+mC)vmin2
联立解得:vmin=$\frac{{v}_{0}}{6}$
答:(1)A离开墙前,弹簧的最大弹性势能Em为$\frac{1}{6}m{v}_{0}^{2}$.
(2)物块A离开墙后,物块C的最小速度vmin为$\frac{{v}_{0}}{6}$.
点评 分析清楚物体的运动过程、正确选择研究对象是正确解题的关键,应用动量守恒定律、机械能守恒定律即可正确解题.

 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | 汤姆孙发现电子,表明原子具有核式结构 | |
| B. | 玻尔在研究原子模型结构中提出了电子云的概念 | |
| C. | 卢瑟福通过对α粒子散射实验,提出原子的核式结构模型 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子总能量减小 |
| A. | 大小1.16kg•m/s,方向与初速度方向相同 | |
| B. | 大小1.16kg•m/s,方向与初速度方向相反 | |
| C. | 大小5.8kg•m/s,方向与初速度方向相同 | |
| D. | 大小5.8kg•m/s,方向与初速度方向相反 |
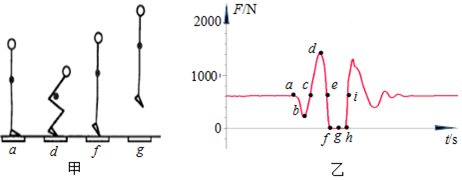
| A. | 乙图中b点时刻,人处于超重状态 | B. | 乙图中d点时刻,人处于失重状态 | ||
| C. | 乙图中g点时刻,人处于失重状态 | D. | 乙图中i点时刻,人的速度为零 |
 如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下级板接地,静电计所带电荷量很少,可被忽略.一带负电油滴静止于电容器中的P点,现将平行板电容器的上极板竖直向上移动一小段距离,则下列判断错误的是( )
如图所示,平行板电容器与电动势为E的直流电源(内阻不计)连接,下级板接地,静电计所带电荷量很少,可被忽略.一带负电油滴静止于电容器中的P点,现将平行板电容器的上极板竖直向上移动一小段距离,则下列判断错误的是( )| A. | 静电计指针张角变小 | |
| B. | P点的电势将降低 | |
| C. | 带电油滴静止不动 | |
| D. | 若先将上极板与电源正极的导线断开,再将下极板向上移动一小段距离,则带电油滴静止不动 |
 如图所示,光滑的平行导轨PQ、MN水平放置,导轨的左右两端分别接定值电阻,R1=R2=4Ω.电阻r=1Ω的金属棒ab与PQ、MN垂直,并接触良好.整个装置处于方向竖直向下、磁感应强度B=1.2T的匀强磁场中.已知平行导轨间距L=0.5m,现对ab施加一水平向右的恒定外力F使之以v=5m/s的速度向右匀速运动,求
如图所示,光滑的平行导轨PQ、MN水平放置,导轨的左右两端分别接定值电阻,R1=R2=4Ω.电阻r=1Ω的金属棒ab与PQ、MN垂直,并接触良好.整个装置处于方向竖直向下、磁感应强度B=1.2T的匀强磁场中.已知平行导轨间距L=0.5m,现对ab施加一水平向右的恒定外力F使之以v=5m/s的速度向右匀速运动,求 跳台滑雪是勇敢者的运动.运动员在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆.如图所示,一位运动员由山坡顶点A以初速度v0=20m/s沿水平方向飞出,落点在山坡上的B点,山坡倾角θ=37°,山坡可以看成一个斜面(g=10m/s2,sin37°=0.6,cos37°=0.8)求:运动员在空中飞行的时间?
跳台滑雪是勇敢者的运动.运动员在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆.如图所示,一位运动员由山坡顶点A以初速度v0=20m/s沿水平方向飞出,落点在山坡上的B点,山坡倾角θ=37°,山坡可以看成一个斜面(g=10m/s2,sin37°=0.6,cos37°=0.8)求:运动员在空中飞行的时间? 如图,在“勇敢向前冲”游戏中,挑战者要通过匀速转动的水平转盘从平台1转移到平台2上,假设挑战者成功跳到转盘上时都能立即与转盘保持相对静止,则挑战者在转盘上距转轴较近的落点A与转盘边缘上的点B一定具有相同的( )
如图,在“勇敢向前冲”游戏中,挑战者要通过匀速转动的水平转盘从平台1转移到平台2上,假设挑战者成功跳到转盘上时都能立即与转盘保持相对静止,则挑战者在转盘上距转轴较近的落点A与转盘边缘上的点B一定具有相同的( )