题目内容
14.若登月宇航员进行以下测量:①当飞船沿贴近月球表面的圆形轨道环绕时,测得环绕周期为T;
②登月舱在月球表面着陆后,宇航员在距月球地面高h处让一小球自由下落,测得小球经过时间t后落地,已知万有引力常量G,h远小于月球半径. 试根据以上测得的量,求:
(1)月球表面的重力加速度g月的大小
(2)月球的半径R.
分析 (1)根据自由落体的高度和时间求得月球表面的重力加速度;
(2)月球表面重力与万有引力相等和万有引力提供近月飞船向心力由飞船周期和重力加速度求出月球的半径R.
解答 解:(1)由题意知,在月球表面h处自由下落的物体经t时间落回地面,由自由落体运动规律有
$h=\frac{1}{2}g{t}^{2}$
可得月球表面的重力加速度g月=$\frac{2h}{{t}^{2}}$
(2)质量为m的飞船在近月面轨道环行时,有:
$G\frac{Mm}{{R}^{2}}=mR(\frac{2π}{T})^{2}$ ①
质量为m的物体在月球表面受到的重力为:
$G\frac{mM}{{R}^{2}}=m{g}_{月}$ ②
代入g月=$\frac{2h}{{t}^{2}}$由①②两式解得:
R=$\frac{h{T}^{2}}{2{π}^{2}{t}^{2}}$
答:(1)月球表面的重力加速度g月的大小为$\frac{2h}{{t}^{2}}$;
(2)月球的半径R为$\frac{h{T}^{2}}{2{π}^{2}{t}^{2}}$.
点评 解决本题的关键是抓住星球表面的重力与万有引力相等,同时万有引力提供环绕天体圆周运动的向心力,这是万有引力应用的两个解决问题的主要入手点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.为了将天上的力和地上的力统一起来,牛顿进行了著名的“月地检验”.“月地检验”比较的是( )
| A. | 月球表面上物体的重力加速度和地球公转的向心加速度 | |
| B. | 月球表面上物体的重力加速度和地球表面上物体的重力加速度 | |
| C. | 月球公转的向心加速度和地球公转的向心加速度 | |
| D. | 月球公转的向心加速度和地球表面上物体的重力加速度 |
9.汽车启动后以额定功率在粗糙的水平公路上运动,下列说法中正确的是( )
| A. | 汽车速率达到最大值之前,加速度是不断增大的 | |
| B. | 汽车速率达到最大值之前,牵引力是不断减小的 | |
| C. | 汽车速率达到最大值之前,汽车做匀加速运动 | |
| D. | 如果路面越粗糙,阻力越大,汽车获得的最终速度也越小 |
19.中国“北斗”卫星导航系统是我国自行研制的全球卫星定位与通信系统,是继美国GPS系统和俄罗斯“格洛纳斯”(GLONASS)系统之后第三个成熟的卫星导航系统.系统由空间端、地面端和用户端组成,其中空间端包括5颗地球同步卫星和30颗非地球同步卫星,以下说法正确的是( )
| A. | 这5颗地球同步卫星的运行速度大于第一宇宙速度 | |
| B. | 这5颗地球同步卫星的运行周期都与地球自转周期相等 | |
| C. | 这5颗地球同步卫星运动的加速度大小不一定相同 | |
| D. | 为避免相撞,不同国家发射的地球同步卫星必须运行在不同的轨道上 |
6. 如图所示,有矩形线圈,面积为S,匝数为N,整个线圈内阻为r,在匀强磁场B 中绕OO′轴以角速度ω匀速转动,外电路电阻为R.当线圈由图示位置转过90°的过程中,下列说法正确的是( )
如图所示,有矩形线圈,面积为S,匝数为N,整个线圈内阻为r,在匀强磁场B 中绕OO′轴以角速度ω匀速转动,外电路电阻为R.当线圈由图示位置转过90°的过程中,下列说法正确的是( )
 如图所示,有矩形线圈,面积为S,匝数为N,整个线圈内阻为r,在匀强磁场B 中绕OO′轴以角速度ω匀速转动,外电路电阻为R.当线圈由图示位置转过90°的过程中,下列说法正确的是( )
如图所示,有矩形线圈,面积为S,匝数为N,整个线圈内阻为r,在匀强磁场B 中绕OO′轴以角速度ω匀速转动,外电路电阻为R.当线圈由图示位置转过90°的过程中,下列说法正确的是( )| A. | 磁通量的变化量为△Φ=NBS | B. | 平均感应电动势为$\overline{E}$=$\frac{2NBSω}{π}$ | ||
| C. | 电阻R所产生的热量为 Q=$\frac{(NBSω\sqrt{2})^{2}}{R}$ | D. | 通过电阻R的电荷量为 q=$\frac{NBS}{R+r}$ |
16.如图甲所示,质量不计的弹簧竖直 固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( ) 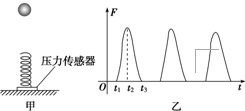

| A. | t1时刻小球动能最大 | |
| B. | t2时刻小球动能为0 | |
| C. | t2~t3这段时间内,小球的动能先减小后增加 | |
| D. | t2~t3这段时间内,小球增加的动能和重力势能之和等于弹簧减少的弹性势能 |
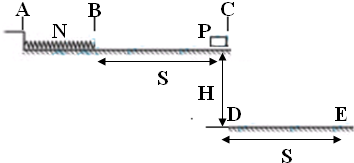
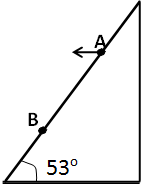 如图所示,在倾角为53°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是S=25m,求:(sin53°=0.8,cos53°=0.6,g=10m/s2)
如图所示,在倾角为53°的斜坡上,从A点水平抛出一个物体,物体落在斜坡的B点,测得AB两点间的距离是S=25m,求:(sin53°=0.8,cos53°=0.6,g=10m/s2)