题目内容
4.人造卫星绕地球做匀速圆周运动,若轨道距地面的高度等于地球半径1.5倍,地球半径为6.4×106m,地面附近的重力加速度g0=π2m/s2,这颗人造地球卫星的周期是2.0×104s.分析 在地球表面重力与万有引力相等,万有引力提供卫星圆周运动向心力展开讨论即可.
解答 解:在地球表面重力与万有引力相等故有:
$G\frac{mM}{{R}^{2}}=m{g}_{0}$
可得GM=${g}_{0}{R}^{2}$
万有引力提供圆周运动向心力有:
$G\frac{mM}{(R+1.5R)^{2}}=m(R+1.5R)\frac{4{π}^{2}}{{T}^{2}}$
可得卫星的周期T=$\sqrt{\frac{4{π}^{2}(R+1.5R)^{3}}{GM}}$=$\sqrt{\frac{4{π}^{2}(2.5R)^{3}}{{g}_{0}{R}^{2}}}$=$\sqrt{\frac{4{π}^{2}2.{5}^{3}{R}^{3}}{{π}^{2}{R}^{2}}}$=$\sqrt{4×2.{5}^{3}×6.4×1{0}^{6}}s=2×1{0}^{4}s$
故答案为:2.0×104s
点评 本题抓住万有引力与重力相等和万有引力提供圆周运动向心力来解决问题,掌握规律是正确解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
1.电源的输出功率P跟外电路的电阻R有关.如图所示,是研究它们关系的实验电路.为了便于进行实验和保护蓄电池,给蓄电池串联了一个定值电阻R0,把它们一起看作新电源(图中虚线框内部分).新电源的内电阻就是蓄电池的内电阻和定值电阻R0之和,用r表示,电源的电动势用E表示.
①写出新电源的输出功率P跟E、r、R的关系式:$P=\frac{{{E^2}R}}{{{{(R+r)}^2}}}$.(安培表、伏特表看作理想电表).
②在实物图中按电路图画出连线,组成实验电路.
③表中给出了6组实验数据,根据这些数据,在方格纸中画出P-R关系图线.根据图线可知,新电源输出功率的最大值约是1.05W,当时对应的外电阻约是5Ω.

①写出新电源的输出功率P跟E、r、R的关系式:$P=\frac{{{E^2}R}}{{{{(R+r)}^2}}}$.(安培表、伏特表看作理想电表).
②在实物图中按电路图画出连线,组成实验电路.
③表中给出了6组实验数据,根据这些数据,在方格纸中画出P-R关系图线.根据图线可知,新电源输出功率的最大值约是1.05W,当时对应的外电阻约是5Ω.
| U(V) | 3.5 | 3.0 | 2.5 | 2.0 | 1.5 | 1.0 |
| I(A) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |

2. 飞行员跳伞后,飞机上其他乘务员(甲)和地面上的人(乙)观察跳伞飞行员的运动后,引发了对跳伞飞行员运动状况的争论.甲认为“跳伞飞行员在沿直线下落”,乙认为“跳伞飞行在沿曲线下落”.下列说法正确是( )
飞行员跳伞后,飞机上其他乘务员(甲)和地面上的人(乙)观察跳伞飞行员的运动后,引发了对跳伞飞行员运动状况的争论.甲认为“跳伞飞行员在沿直线下落”,乙认为“跳伞飞行在沿曲线下落”.下列说法正确是( )
 飞行员跳伞后,飞机上其他乘务员(甲)和地面上的人(乙)观察跳伞飞行员的运动后,引发了对跳伞飞行员运动状况的争论.甲认为“跳伞飞行员在沿直线下落”,乙认为“跳伞飞行在沿曲线下落”.下列说法正确是( )
飞行员跳伞后,飞机上其他乘务员(甲)和地面上的人(乙)观察跳伞飞行员的运动后,引发了对跳伞飞行员运动状况的争论.甲认为“跳伞飞行员在沿直线下落”,乙认为“跳伞飞行在沿曲线下落”.下列说法正确是( )| A. | 如果以地面为参考系,甲的说法是正确的 | |
| B. | 甲、乙争论是由于选择不同的参考系引起的 | |
| C. | 研究物体的运动时,需要选择合适的参考系 | |
| D. | 参考系的选择只能是相对于地面静止的物体 |
12.在河面上方h=20m的岸上,有人用绕过滑轮(可视为质点)的细长绳拴住一条小船,绳与水平面的夹角为30°,接着人以恒定的速率v=3m/s拉绳,使小船靠岸,那么( )
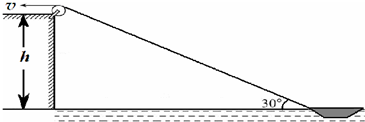

| A. | 5 s时绳与水面的夹角为60° | B. | 5 s后小船前进了15 m | ||
| C. | 5 s时小船的速率为4 m/s | D. | 5 s时小船到岸边的距离为15 m |
19.做匀速圆周运动的物体,圆半径为R,转动频率为f,转速为n,以下说法正确的是( )
| A. | 线速度v=$\frac{2πR}{f}$ | B. | 线速度v=2nπR | C. | 角速度ω=2πfn | D. | 角速度ω=$\frac{2nπ}{f}$ |
9.下列说法中正确的是( )
| A. | 在水平地面以上某高度的物体重力势能一定为正值 | |
| B. | 在水平地面以下某高度的物体重力势能为负值 | |
| C. | 不同的物体中离地面最高的物体其重力势能最大 | |
| D. | 离地面有一定高度的物体其重力势能可能为零 |
13. 如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动,运动中始终保持悬线竖直,下列说法正确的是( )
如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动,运动中始终保持悬线竖直,下列说法正确的是( )
 如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动,运动中始终保持悬线竖直,下列说法正确的是( )
如图所示,一块橡皮用细线悬挂于O点,用钉子靠着线的左侧,沿与水平方向成30°角的斜面向右以速度v匀速运动,运动中始终保持悬线竖直,下列说法正确的是( )| A. | 橡皮的速度大小为$\sqrt{2}$v | B. | 橡皮的速度大小为$\sqrt{3}$v | ||
| C. | 橡皮的速度与水平方向成30°角 | D. | 橡皮的速度与水平方向成45°角 |
14.光滑绝缘水平面上有甲,乙,丙三点位于同一直线上,甲在左,乙在中,丙在右.且甲乙的距离大于乙丙的距离.A,B,C三个带电体分别位于甲乙丙三点.为使三个自由电荷都保持静止,它们的电量可能是( )
| A. | QA=25×10-3c QB=-4×10-3c QC=-9×10-3c | |
| B. | QA=36×10-3c QB=-4×10-3c QC=9×10-3c | |
| C. | QA=4×10-3c QB=-5×10-3c QC=1×10-3c | |
| D. | QA=16×10-3c QB=-2×10-3c QC=24×10-3c |