题目内容
10.一辆执勤的警车停在直公路边,当警员发现前方以v=10m/s的速度匀速行驶的货车有违章行为时,决定前去追赶,立即警车发动起来,以加速度a=2m/s2做匀加速运动,问:(1)在警车追上货车之前,两车间的最大距离是多少?
(2)警车发动起来后一直做匀加速运动,则至少要多长时间才能追上违章的货车?
分析 (1)当两车速度相等时,相距最远,结合速度时间公式求出速度相等经历的时间,根据位移关系求出两车间的最大距离.
(2)根据位移关系,结合运动学公式求出追及的时间.
解答 解:(1)两车间距离最大时:v警=v=at1
解得${t}_{1}=\frac{v}{a}=\frac{10}{2}s=5s$,
此时警车的位移${x}_{1}=\frac{v}{2}×{t}_{1}=\frac{10}{2}×5m=25m$,
违章车的位移x2=vt1=10×5m=50m,
则两车间的最大距离△x=x2-x1=50-25m=25m.
(2)设至少经过t时间才能追上违章的货车,
则有:$\frac{1}{2}a{t}^{2}=vt$,解得t=$\frac{2v}{a}=\frac{2×10}{2}s=10s$.
答:(1)在警车追上货车之前,两车间的最大距离是25m.
(2)至少要10s时间才能追上违章的货车.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时,两车有最大距离.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
20.由于地球自转,又由于地球的极半径较短而赤道半径较长,使得在地球表面的同一物体受到的重力( )
| A. | 在两极较大 | B. | 在赤道较大 | ||
| C. | 在两极跟在赤道一样大 | D. | 无法判断 |
1.竖直升空的火箭,其速度图象如图所示,由图可知( )


| A. | 火箭上升到最高点所用的时间是120s | |
| B. | 火箭前40s上升,以后下降 | |
| C. | 燃料用完时,火箭离地高度是48000m | |
| D. | 火箭的加速度开始是20m/s2,之后加速度变为-10m/s2 |
2.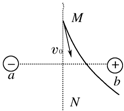 在图中,a、b带等量异种电荷,MN为ab连线的中垂线,现有一个带电粒子从M点以一定初速度v0射入,开始时一段轨迹如图中实线,不考虑粒子重力,则下列有关粒子在飞越该电场的整个过程中的说法不正确的是( )
在图中,a、b带等量异种电荷,MN为ab连线的中垂线,现有一个带电粒子从M点以一定初速度v0射入,开始时一段轨迹如图中实线,不考虑粒子重力,则下列有关粒子在飞越该电场的整个过程中的说法不正确的是( )
 在图中,a、b带等量异种电荷,MN为ab连线的中垂线,现有一个带电粒子从M点以一定初速度v0射入,开始时一段轨迹如图中实线,不考虑粒子重力,则下列有关粒子在飞越该电场的整个过程中的说法不正确的是( )
在图中,a、b带等量异种电荷,MN为ab连线的中垂线,现有一个带电粒子从M点以一定初速度v0射入,开始时一段轨迹如图中实线,不考虑粒子重力,则下列有关粒子在飞越该电场的整个过程中的说法不正确的是( )| A. | 该粒子带负电 | |
| B. | 该粒子的动能先增大,后减小 | |
| C. | 该粒子所经位置的电势先降低,后升高 | |
| D. | 该粒子运动到无穷远处后,速度的大小一定仍为v0 |
19.下列说法正确的是( )
| A. | 在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此,光子散射后波长变长 | |
| B. | 考古学家发现某一骸骨中碳14的含量为活着的生物含量的四分之一,已知碳14的半衰期为5730年,则确定该生物死亡距今11460年 | |
| C. | 按照波尔理论,氢原子核外电子从较小半径跃迁到较大半径轨道时,电子的动能减少,原子总能量增大 | |
| D. | 卢瑟福发现了中子,汤姆孙发现了电子 | |
| E. | 机场、车站等地方进行安检工作时,能轻而易举地窥见箱内物品,利用了γ射线较强的穿透能力 |
14.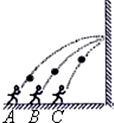 壁球是一种对墙击球的室内运动,如图所示,一同学分别在同一直线上的A、B、C三个位置击打壁球,结果都垂直击中墙壁同一位置.球飞出的速度分别为v1、v2、v3.若三次壁球击打点的高度均相同,球飞出的方向与水平方向夹角分别为θ1、θ2、θ3,则下列说法正确的是( )
壁球是一种对墙击球的室内运动,如图所示,一同学分别在同一直线上的A、B、C三个位置击打壁球,结果都垂直击中墙壁同一位置.球飞出的速度分别为v1、v2、v3.若三次壁球击打点的高度均相同,球飞出的方向与水平方向夹角分别为θ1、θ2、θ3,则下列说法正确的是( )
 壁球是一种对墙击球的室内运动,如图所示,一同学分别在同一直线上的A、B、C三个位置击打壁球,结果都垂直击中墙壁同一位置.球飞出的速度分别为v1、v2、v3.若三次壁球击打点的高度均相同,球飞出的方向与水平方向夹角分别为θ1、θ2、θ3,则下列说法正确的是( )
壁球是一种对墙击球的室内运动,如图所示,一同学分别在同一直线上的A、B、C三个位置击打壁球,结果都垂直击中墙壁同一位置.球飞出的速度分别为v1、v2、v3.若三次壁球击打点的高度均相同,球飞出的方向与水平方向夹角分别为θ1、θ2、θ3,则下列说法正确的是( )| A. | v1<v2<v3 | B. | θ1<θ2<θ3 | C. | v1>v2>v3 | D. | θ1>θ2>θ3 |
 一放在水平面上的物体,重量为30N,受到一个斜向上的与水平面成37度角的拉力F的作用,在水平面上匀速运动,拉力F的大小为10N.求物体与水平面间的摩擦因数.
一放在水平面上的物体,重量为30N,受到一个斜向上的与水平面成37度角的拉力F的作用,在水平面上匀速运动,拉力F的大小为10N.求物体与水平面间的摩擦因数.