题目内容
14.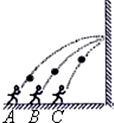 壁球是一种对墙击球的室内运动,如图所示,一同学分别在同一直线上的A、B、C三个位置击打壁球,结果都垂直击中墙壁同一位置.球飞出的速度分别为v1、v2、v3.若三次壁球击打点的高度均相同,球飞出的方向与水平方向夹角分别为θ1、θ2、θ3,则下列说法正确的是( )
壁球是一种对墙击球的室内运动,如图所示,一同学分别在同一直线上的A、B、C三个位置击打壁球,结果都垂直击中墙壁同一位置.球飞出的速度分别为v1、v2、v3.若三次壁球击打点的高度均相同,球飞出的方向与水平方向夹角分别为θ1、θ2、θ3,则下列说法正确的是( )| A. | v1<v2<v3 | B. | θ1<θ2<θ3 | C. | v1>v2>v3 | D. | θ1>θ2>θ3 |
分析 据题知三个壁球都垂直击中墙壁,其逆过程是平抛运动,它们上升的高度相等,水平位移大小不等,根据平抛运动的规律得到水平位移与初速度的关系,分析初速度的大小.结合平行四边形定则得出抛出时的速度大小,根据速度的分解,分析角度的关系.
解答 解:A、三个壁球都垂直击中墙壁,其逆过程是平抛运动,设任一篮球击中篮筐的速度v,上升的高度为h,水平位移为x.
根据h=$\frac{1}{2}g{t}^{2}$知,运动的时间相同,由于xA>xB>xc,则v01>v02>v03,
高度相同,则抛出时的竖直分速度相等,根据平行四边形定则知,v1>v2>v3.故A错误,C正确.
B、根据平行四边形定则知,$tanθ=\frac{{v}_{y}}{{v}_{0}}$,由于竖直分速度相等,可知θ1<θ2<θ3,故B正确,D错误.
故选:BC.
点评 本题运用逆向思维研究斜抛运动,关键是要明确平抛运动的研究方法、位移公式和速度公式,是解决平抛运动问题的基础知识.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.关于匀强电场电场强度和电势差的关系,下列说法正确的是( )
| A. | 在相同距离上的两点,电势差大的其场强也必定大 | |
| B. | 沿电场线的方向,任何相等距离上的电势降落必定相等 | |
| C. | 场强在数值上等于每单位距离上的电势的降落 | |
| D. | 电势降低的方向必定是电场强度的方向 |
2.一负试探电荷的电荷量为10-10C,放在电场中的P点,所受电场力大小为10-6N,方向向东,则P点的场强为( )
| A. | 104N/C,方向向西 | B. | 104N/C,方向向东 | ||
| C. | 10-4N/C,方向向西 | D. | 10-4N/C,方向向东 |
6.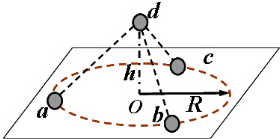 如图所示,a、b、c、d四个质量均为m的带电小球恰好构成“三星拱月”之形,其中a、b、c上完全相同的带电小球在光滑绝缘水平面内的同一圆周上绕O点做半径为R的匀速圆周运动,三小球所在位置恰好将圆周等分.小球d位于O点正上方h处,且在外力F作用下恰处于静止状态,已知a、b、c三小球的电荷量均为q,d球的电荷量为6q,h=$\sqrt{2}$R.重力加速度为g,静电力常量为k,则( )
如图所示,a、b、c、d四个质量均为m的带电小球恰好构成“三星拱月”之形,其中a、b、c上完全相同的带电小球在光滑绝缘水平面内的同一圆周上绕O点做半径为R的匀速圆周运动,三小球所在位置恰好将圆周等分.小球d位于O点正上方h处,且在外力F作用下恰处于静止状态,已知a、b、c三小球的电荷量均为q,d球的电荷量为6q,h=$\sqrt{2}$R.重力加速度为g,静电力常量为k,则( )
 如图所示,a、b、c、d四个质量均为m的带电小球恰好构成“三星拱月”之形,其中a、b、c上完全相同的带电小球在光滑绝缘水平面内的同一圆周上绕O点做半径为R的匀速圆周运动,三小球所在位置恰好将圆周等分.小球d位于O点正上方h处,且在外力F作用下恰处于静止状态,已知a、b、c三小球的电荷量均为q,d球的电荷量为6q,h=$\sqrt{2}$R.重力加速度为g,静电力常量为k,则( )
如图所示,a、b、c、d四个质量均为m的带电小球恰好构成“三星拱月”之形,其中a、b、c上完全相同的带电小球在光滑绝缘水平面内的同一圆周上绕O点做半径为R的匀速圆周运动,三小球所在位置恰好将圆周等分.小球d位于O点正上方h处,且在外力F作用下恰处于静止状态,已知a、b、c三小球的电荷量均为q,d球的电荷量为6q,h=$\sqrt{2}$R.重力加速度为g,静电力常量为k,则( )| A. | 小球a一定带正电 | |
| B. | 小球b的周期为$\frac{2πR}{q}$$\sqrt{\frac{mR}{k}}$ | |
| C. | 小球c的加速度大小为$\frac{\sqrt{3}k{q}^{2}}{3m{R}^{2}}$ | |
| D. | 外力F竖直向上,大小等于mg+$\frac{2\sqrt{6}k{q}^{2}}{{R}^{2}}$ |
3.“探究加速度与力、质量关系”的实验装置如图1所示.

(1)下列说法正确的是CD
A.平衡摩擦力时,要用细绳把装砂的小桶通过定滑轮拴在小车上
B.平衡摩擦力后,如果改变了小车上砝码的数量,应重新平衡摩擦力
C.要将小桶和砂子的总重力mg当做小车(质量为M)受到的细绳拉力,必须使M》m
D.实验时应先接通电源再释放小车
(2)某同学在没有平衡摩擦力的情况下,保持小车及砝码的质量不变,测得5组小车加速度a和拉力F的数据如表所示.
据测得的数据作出a-F图象并由图象得出以下两个数据:(结果保留两位有效数字).
①小车与长木板之间的最大静摩擦力大小为0.10N;
②小车的质量为1.0kg.

(1)下列说法正确的是CD
A.平衡摩擦力时,要用细绳把装砂的小桶通过定滑轮拴在小车上
B.平衡摩擦力后,如果改变了小车上砝码的数量,应重新平衡摩擦力
C.要将小桶和砂子的总重力mg当做小车(质量为M)受到的细绳拉力,必须使M》m
D.实验时应先接通电源再释放小车
(2)某同学在没有平衡摩擦力的情况下,保持小车及砝码的质量不变,测得5组小车加速度a和拉力F的数据如表所示.
| F(N) | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a(m/s2) | 0.10 | 0.21 | 0.29 | 0.32 | 0.49 |
①小车与长木板之间的最大静摩擦力大小为0.10N;
②小车的质量为1.0kg.
4.弹簧振子在做机械振动时,按周期性规律变化的物理量是( )
| A. | 回复力 | B. | 周期 | C. | 频率 | D. | 振幅 |

 从倾角为θ的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,其落点与A的水平距离为x1,若将水平抛出时的速度改为2v0,则落点与A的水平距离为x2,球下面两种情况下x1:x2的值分别是多大?
从倾角为θ的斜面上A点,以水平速度v0抛出一个小球,不计空气阻力,其落点与A的水平距离为x1,若将水平抛出时的速度改为2v0,则落点与A的水平距离为x2,球下面两种情况下x1:x2的值分别是多大?