题目内容
2.火箭在水平飞行过程中的某段极短时间△t内向后喷出的燃气质量为△m,喷出的燃气相对喷气前火箭的速度是u,喷出燃气后火箭的质量为m,已知火箭飞行区域的重力加速度为g,则下列结论不正确的是( )| A. | 这段时间内火箭速度的增加量大小△v=$\frac{{△}_{m}}{m}$u | |
| B. | 这段时间内燃气对火箭的平均作用力大小F=$\frac{{△}_{m}}{{△}_{t}}$u+mg | |
| C. | 这段时间内火箭的平均加速度大小a=$\frac{{△}_{m}}{m{△}_{t}}$u | |
| D. | 这段时间内火箭对燃气的冲量大小I=△mu |
分析 对火箭和气体系统为研究对象,在水平方向上运用动量守恒定律,求出喷气后火箭增加的速度,由动量定理求出平均作用力,由牛顿第二定律求出加速度.
解答 解:A、设火箭开始时的速度为v0,以火箭飞行的方向为正方向,在水平方向火箭与气体组成的系统的动量是守恒的,根据动量守恒定律得:
(m+△m)v0=△m(v0-u)+m(v0+△v)
解得:△v=$\frac{△mu}{m}$.故A正确;
B、这段时间内燃气对火箭的平均作用力的冲量等于火箭动量的变化,根据动量定理得:
m△v=F•△t
所以:F=$\frac{△mu}{t}$.故B错误;
C、由牛顿第二定律,这段时间内火箭的平均加速度大小a=$\frac{F}{m}=\frac{△mu}{mt}$.故C正确;
D、根据动量定理可知,这段时间内火箭对燃气的冲量大小I=△mu.故D正确.
本题选择不正确的,故选:B
点评 解决本题的关键知道系统在水平方向上动量守恒,结合动量定理进行求解.

练习册系列答案
相关题目
15. 如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )
如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )
 如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )
如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )| A. | 分子之间存在着引力 | B. | 分子之间存在着斥力 | ||
| C. | 引力和斥力是同时存在的 | D. | 分子在永不停息地做无规则热运动 |
14.交变电源与R=10Ω的电阻连接,电源输出电压u随时间t变化的图象如下,则( )

| A. | R两端电压uR随时间t变化的规律是uR=5$\sqrt{2}$cos50πt(V) | |
| B. | R两端电压uR随时间t变化的规律是uR=10$\sqrt{2}$cos50πt(V) | |
| C. | 通过R的电流iR随时间t变化的规律是iR=$\sqrt{2}$cos100πt(V) | |
| D. | 通过R的电流iR随时间t变化的规律是iR=cos100πt(A) |
11.关于原子结构和玻尔理论,下列说法中正确的是( )
| A. | 汤姆孙发现电子,表明原子具有核式结构 | |
| B. | 玻尔在研究原子模型结构中提出了电子云的概念 | |
| C. | 卢瑟福通过对α粒子散射实验,提出原子的核式结构模型 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子总能量减小 |

 如图所示,光滑的平行导轨PQ、MN水平放置,导轨的左右两端分别接定值电阻,R1=R2=4Ω.电阻r=1Ω的金属棒ab与PQ、MN垂直,并接触良好.整个装置处于方向竖直向下、磁感应强度B=1.2T的匀强磁场中.已知平行导轨间距L=0.5m,现对ab施加一水平向右的恒定外力F使之以v=5m/s的速度向右匀速运动,求
如图所示,光滑的平行导轨PQ、MN水平放置,导轨的左右两端分别接定值电阻,R1=R2=4Ω.电阻r=1Ω的金属棒ab与PQ、MN垂直,并接触良好.整个装置处于方向竖直向下、磁感应强度B=1.2T的匀强磁场中.已知平行导轨间距L=0.5m,现对ab施加一水平向右的恒定外力F使之以v=5m/s的速度向右匀速运动,求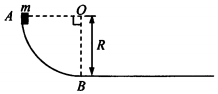 AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平长直轨道相切,如图所示.一小木块(可视为质点)自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小木块的质量为m,与水平轨道的动摩擦因数为μ,重力加速度为g.求:
AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平长直轨道相切,如图所示.一小木块(可视为质点)自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小木块的质量为m,与水平轨道的动摩擦因数为μ,重力加速度为g.求: