题目内容
5. 如图所示,平行金属导轨与水平面间的倾角为θ(导轨的电阻不计),与阻值为R的定值电阻相连.磁感应强度为B匀强磁场垂直穿过导轨道平面.有一质量为m、长为L的导体棒从ab位置获得平行斜面向上、大小为v的初速度向上运动,最远到达a′b′,滑行的距离为s,导体棒的电阻也为R,棒与导轨的动摩擦因数为μ.则( )
如图所示,平行金属导轨与水平面间的倾角为θ(导轨的电阻不计),与阻值为R的定值电阻相连.磁感应强度为B匀强磁场垂直穿过导轨道平面.有一质量为m、长为L的导体棒从ab位置获得平行斜面向上、大小为v的初速度向上运动,最远到达a′b′,滑行的距离为s,导体棒的电阻也为R,棒与导轨的动摩擦因数为μ.则( )| A. | 上滑过程中导体棒做匀减速运动 | |
| B. | 上滑过程中,安培力、滑动摩擦力和重力对导体棒所做的总功为-$\frac{1}{2}$mv2 | |
| C. | 上滑过程中回路产生的焦耳热为$\frac{1}{2}$mv2-mgs(sinθ+μcosθ) | |
| D. | 上滑过程中导体棒损失的机械能为$\frac{1}{2}$mv2-mgssinθ |
分析 导体棒向上做减速运动,开始时速度最大,产生的感应电流最大,受到的安培力最大,由E=BLv、I=$\frac{E}{2R}$、FA=BIL求出最大安培力.根据动能定理分析总功.由能量守恒定律研究热量.上滑的过程中动能减小,重力势能增加,即可求得机械能的损失.
解答 解:A、导体棒开始运动时所受的安培力最大,由E=BLv、I=$\frac{E}{2R}$、FA=BIL得到最大安培力为FA=$\frac{{B}^{2}{L}^{2}v}{2R}$,由于安培力与速度成正比,所以随速度的减小安培力减小,导体棒向上做加速度减小的减速运动.故A错误.
B、导体棒上滑的过程中,根据动能定理得知,安培力、滑动摩擦力和重力对导体棒做的总功为-$\frac{1}{2}m{v^2}$.故B正确.
C、根据能量守恒可知,上滑过程中导体棒的动能减小,转化为焦耳热、摩擦生热和重力势能,则有电流做功发出的热量为Q=$\frac{1}{2}m{v^2}$-mgs(sinθ+μcosθ).故C正确.
D、上滑的过程中导体棒的动能减小$\frac{1}{2}m{v}^{2}$,重力势能增加mgs sinθ,所以导体棒损失的机械能为$\frac{1}{2}m{v^2}$-mgssinθ.故D正确.
故选:BCD
点评 在推导安培力时要掌握安培力的一般表达式F=$\frac{{B}^{2}{L}^{2}v}{R+r}$,R+r是回路的总电阻,导体棒的电阻不能遗漏.要抓住能量如何转化的,分析热量.

练习册系列答案
相关题目
15. 如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )
如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )
 如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )
如图所示,把两块平整的铅块压紧使它们“粘”在一起,甚至在下面吊一个钩码也不能把它们拉开,这说明( )| A. | 分子之间存在着引力 | B. | 分子之间存在着斥力 | ||
| C. | 引力和斥力是同时存在的 | D. | 分子在永不停息地做无规则热运动 |
2.下列情况中,运动物体机械能一定守恒的是( )
| A. | 作匀速直线运动的物体 | B. | 作平抛运动的物体 | ||
| C. | 只受重力作用的物体 | D. | 不受摩擦力作用的物体 |
14.交变电源与R=10Ω的电阻连接,电源输出电压u随时间t变化的图象如下,则( )

| A. | R两端电压uR随时间t变化的规律是uR=5$\sqrt{2}$cos50πt(V) | |
| B. | R两端电压uR随时间t变化的规律是uR=10$\sqrt{2}$cos50πt(V) | |
| C. | 通过R的电流iR随时间t变化的规律是iR=$\sqrt{2}$cos100πt(V) | |
| D. | 通过R的电流iR随时间t变化的规律是iR=cos100πt(A) |
15.如图所示,甲图是某人站在力传感器上做下蹲-起跳动作的示意图,甲图中的“●”表示人的重心,乙图是根据力传感器画出的压力F随时间t变化的图线.乙图中a、d、f、g各点数据分别与甲图中人的a、d、f、g状态相对应,其余点对应状态没有在甲图中画出.乙图中a、c、e、i点对应的纵坐标均为610N.请根据这两个图所给出的信息,判断下列说法中正确的是( )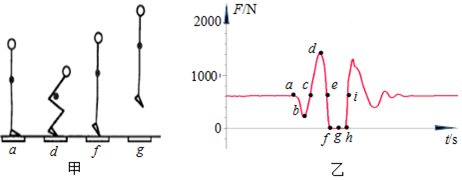

| A. | 乙图中b点时刻,人处于超重状态 | B. | 乙图中d点时刻,人处于失重状态 | ||
| C. | 乙图中g点时刻,人处于失重状态 | D. | 乙图中i点时刻,人的速度为零 |
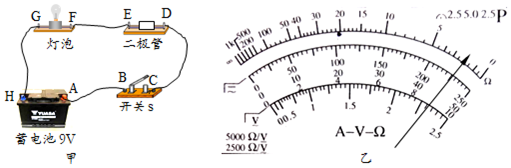
 如图所示,光滑的平行导轨PQ、MN水平放置,导轨的左右两端分别接定值电阻,R1=R2=4Ω.电阻r=1Ω的金属棒ab与PQ、MN垂直,并接触良好.整个装置处于方向竖直向下、磁感应强度B=1.2T的匀强磁场中.已知平行导轨间距L=0.5m,现对ab施加一水平向右的恒定外力F使之以v=5m/s的速度向右匀速运动,求
如图所示,光滑的平行导轨PQ、MN水平放置,导轨的左右两端分别接定值电阻,R1=R2=4Ω.电阻r=1Ω的金属棒ab与PQ、MN垂直,并接触良好.整个装置处于方向竖直向下、磁感应强度B=1.2T的匀强磁场中.已知平行导轨间距L=0.5m,现对ab施加一水平向右的恒定外力F使之以v=5m/s的速度向右匀速运动,求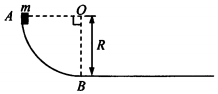 AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平长直轨道相切,如图所示.一小木块(可视为质点)自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小木块的质量为m,与水平轨道的动摩擦因数为μ,重力加速度为g.求:
AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平长直轨道相切,如图所示.一小木块(可视为质点)自A点起由静止开始沿轨道下滑.已知圆轨道半径为R,小木块的质量为m,与水平轨道的动摩擦因数为μ,重力加速度为g.求: