题目内容
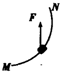
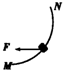
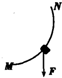
15. 如图示,在不计摩擦力时小球从高h处自由滚下进入竖直圆环轨道,圆环轨道半径为R,则下列说法中正确的是( )
如图示,在不计摩擦力时小球从高h处自由滚下进入竖直圆环轨道,圆环轨道半径为R,则下列说法中正确的是( )| A. | 当h≥$\frac{5}{2}$R时,小球一定能通过环顶 | |
| B. | 当R<h<$\frac{5}{2}$R时,小球一定在上半环某处脱离轨道 | |
| C. | 只要小球能通过环顶,小球在环顶与环底的压力差一定为6mg | |
| D. | 只要小球能通过环顶,小球在环底在最小加速度必为4g |
分析 不计摩擦力,小球在圆形的内轨道运动,通过最高点的临界情况是弹力为零,靠重力提供向心力,根据牛顿第二定律求出临界速度,再根据动能定理求出小球开始下落的最小高度.
解答 解:A、在最高点的临界情况为:mg=m $\frac{{v}^{2}}{R}$,解得v=$\sqrt{gR}$.根据动能定理得:mg(h-2R)=$\frac{1}{2}$mv2,解得h=$\frac{5}{2}$R.所以当h≥$\frac{5}{2}$R时,小球一定能通过环顶.故A正确.
B、当h>R时,根据动能定理知,小球一定能越过$\frac{1}{4}$圆周,所以当R<h<$\frac{5}{2}$R时,小球一定在上半环某处脱离轨道.故B正确.
C、在最高点有:mg+N1=m$\frac{{v}_{1}^{2}}{R}$,在最低点有:N2-mg=m$\frac{{v}_{2}^{2}}{R}$,根据动能定理有:mg•2R=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12,联立三式解得:N2-N1=6mg.故C正确.
D、当小球恰好越过最高点时,v=$\sqrt{gR}$.根据动能定理,mg•2R=$\frac{1}{2}$mv′2-$\frac{1}{2}$mv2,由a=$\frac{v{′}^{2}}{R}$得,a=5g.在最低点的最小加速度为5g.故D错误.
故选:ABC.
点评 本题综合考查了牛顿第二定律和动能定理,关键理清向心力的来源,选择动能定理或机械能守恒定律结合进行求解.

练习册系列答案
相关题目
5.某人从高处跳下落至地面上,在脚与地面接触的这段时间内,下列说法正确的是( )
| A. | 人对地面的压力大于人受的重力 | |
| B. | 地面对人的弹力大于人对地面的压力 | |
| C. | 地面对人的弹力大小等于人对地面的压力 | |
| D. | 地面对人的弹力小于人对地面的压力 |
6. 如图所示,A为长木板,在水平面上以速度v1(相对地面)向右运动,B为滑块,以速度v2(相对地面)向右运动.以下说法中正确的是( )
如图所示,A为长木板,在水平面上以速度v1(相对地面)向右运动,B为滑块,以速度v2(相对地面)向右运动.以下说法中正确的是( )
 如图所示,A为长木板,在水平面上以速度v1(相对地面)向右运动,B为滑块,以速度v2(相对地面)向右运动.以下说法中正确的是( )
如图所示,A为长木板,在水平面上以速度v1(相对地面)向右运动,B为滑块,以速度v2(相对地面)向右运动.以下说法中正确的是( )| A. | 若v1=v2,则A、B间无滑动摩擦力 | |
| B. | 若v1>v2,则B对A有向右的滑动摩擦力 | |
| C. | 若v1>v2,则A对B有向右的滑动摩擦力 | |
| D. | 若v1<v2,则A对B有向右的滑动摩擦力 |
10.下列说法中正确的是( )
| A. | 总结出关于行星运动三条定律的科学家是开普勒 | |
| B. | 总结出万有引力定律的物理学家是伽俐略 | |
| C. | 总结出万有引力定律的物理学家是卡文迪许 | |
| D. | 第一次精确测量出万有引力常量的物理学家是牛顿 |
7.下列叙述正确的是( )
| A. | 悬浮在液体中的固体微粒越大,布朗运动就越明显 | |
| B. | 物体的温度越高,分子热运动的平均动能越大 | |
| C. | 当分子间的距离增大时,分子间的引力变大而斥力减小 | |
| D. | 物体的速度越大,内部分子的热运动越激烈 |
4. 三个质点甲、乙、丙在同一平面内同时自同一位置出发,经相同时间后又相遇在同一位置,运动的轨迹示意图,这段时间它们的平均速度分别为$\overline{{v}_{1}}$、$\overline{{v}_{2}}$、$\overline{{v}_{3}}$,平均速率分别为$\overline{{u}_{1}}$、$\overline{{u}_{2}}$、$\overline{{u}_{3}}$,下列说法中正确的是( )
三个质点甲、乙、丙在同一平面内同时自同一位置出发,经相同时间后又相遇在同一位置,运动的轨迹示意图,这段时间它们的平均速度分别为$\overline{{v}_{1}}$、$\overline{{v}_{2}}$、$\overline{{v}_{3}}$,平均速率分别为$\overline{{u}_{1}}$、$\overline{{u}_{2}}$、$\overline{{u}_{3}}$,下列说法中正确的是( )
 三个质点甲、乙、丙在同一平面内同时自同一位置出发,经相同时间后又相遇在同一位置,运动的轨迹示意图,这段时间它们的平均速度分别为$\overline{{v}_{1}}$、$\overline{{v}_{2}}$、$\overline{{v}_{3}}$,平均速率分别为$\overline{{u}_{1}}$、$\overline{{u}_{2}}$、$\overline{{u}_{3}}$,下列说法中正确的是( )
三个质点甲、乙、丙在同一平面内同时自同一位置出发,经相同时间后又相遇在同一位置,运动的轨迹示意图,这段时间它们的平均速度分别为$\overline{{v}_{1}}$、$\overline{{v}_{2}}$、$\overline{{v}_{3}}$,平均速率分别为$\overline{{u}_{1}}$、$\overline{{u}_{2}}$、$\overline{{u}_{3}}$,下列说法中正确的是( )| A. | $\overline{{v}_{1}}$>$\overline{{v}_{3}}$>$\overline{{v}_{2}}$ | B. | $\overline{{v}_{1}}$=$\overline{{v}_{3}}$=$\overline{{v}_{2}}$ | C. | $\overline{{u}_{1}}$>$\overline{{u}_{3}}$>$\overline{{u}_{2}}$ | D. | $\overline{{u}_{1}}$=$\overline{{u}_{2}}$=$\overline{{u}_{3}}$ |
5. 如图所示,AB为斜面,倾角为30°,小球从A点以9.8$\sqrt{3}$m/s的速度水平抛出,恰好落到B点,忽略空气阻力,则物体在空中飞行的时间为( )
如图所示,AB为斜面,倾角为30°,小球从A点以9.8$\sqrt{3}$m/s的速度水平抛出,恰好落到B点,忽略空气阻力,则物体在空中飞行的时间为( )
 如图所示,AB为斜面,倾角为30°,小球从A点以9.8$\sqrt{3}$m/s的速度水平抛出,恰好落到B点,忽略空气阻力,则物体在空中飞行的时间为( )
如图所示,AB为斜面,倾角为30°,小球从A点以9.8$\sqrt{3}$m/s的速度水平抛出,恰好落到B点,忽略空气阻力,则物体在空中飞行的时间为( )| A. | 9.8s | B. | 1s | C. | 2s | D. | $\sqrt{3}$s |
 如图所示,质点P受到三个共点力的作用.F1=20N,F2=50N,F3=40N,F1与F2在一条直线上且与F3垂直.
如图所示,质点P受到三个共点力的作用.F1=20N,F2=50N,F3=40N,F1与F2在一条直线上且与F3垂直.