题目内容
15.质量是0.2kg的物块放在倾角为37°的斜面底端,在沿斜面向上方向大小为2N的力F的作用下,由静止开始沿斜面向上滑动了4m,然后撤去力F,已知物块跟斜面间的摩擦因数是0.25,g取10m/s2.求:(1)物块还能沿斜面上升多长时间?
(2)物体回到斜面底端的速度.
分析 此题的物理过程看起来简短,但后一过程即撤去外力后先匀减速至零,返回时做匀加速运动,应该是三个过程.
(1)有拉力时,加速过程是已知力求运动,即末速度和上升的位移.撤去外力后,由于受到重力和摩擦力作用,物体将向上匀减速运动,直到速度为零.据牛顿运动定律求出加速度,再根据运动学规律求时间和位移.
(2)返回时,物体做匀加运动,同样是已知运动求力,只是加速发生变化,总位移是上升过程两个阶段的位移之和.
解答 解:(1)有拉力时,物体向上做匀加速运动,据牛顿第二定律求得加速度:
${a}_{1}=\frac{F-mgsin37°-μmgcos37°}{m}=\frac{2-0.2×10×0.6-0.25×0.2×10×0.8}{0.2}=2m/{s}^{2}$
经过x=4m的加速后,经历的时间:
${t}_{1}=\sqrt{\frac{2x}{{a}_{1}}}=\sqrt{\frac{2×4}{2}}s=2s$
向上加速的位移:
${x}_{1}=\frac{1}{2}{a}_{1}{{t}_{1}}^{2}=\frac{1}{2}×2×{2}^{2}m=4m$
此过程的末速度:
v1=a1t1=2×2m/s=4m/s
撤去外力后,物体向上匀减速的加速度:
${a}_{2}=gsin37°+μgcos37°=(10×0.6+0.25×10×0.8)m/{s}^{2}=8m/{s}^{2}$
减速到零的时间:
${t}_{2}=\frac{0-{v}_{1}}{-{a}_{1}}=\frac{0-4}{-8}s=0.5s$
所以,还能沿斜面上升的时间为0.5s
还可求出还能向上滑行的距离:
${x}_{2}=\frac{0-{{v}_{1}}^{2}}{-2{a}_{2}}=\frac{{4}^{2}}{2×8}m=1m$
(2)之后物体沿斜面向下做匀加速运动,加速度:
${a}_{3}=gsin37°-μgcos37°=4m/{s}^{2}$
到达斜面底端的位移:
x3=x1+x2=5m
到达底端的速度:
${v}_{3}=\sqrt{2{a}_{3}{x}_{3}}=\sqrt{2×4×5}m/s=4.47m/s$
答:(1)物块还能沿斜面上升时间为0.5s
(2)物体回到斜面底端的速度为4.47m/s
点评 此题三个过程均是已知受力求运动,先根据牛顿第二定律求出加速度,再根据运动学规律求相关运动量.注意三个过程的加速度均不相同、前一过程的末状态是后一状态的初状态、前两个过程的总位移是最后一个过程的位移.这种题型只能算完前一过程量,再向下继续.

①测量前应检查指针是否停在“Ω”刻度线的“∞”处;
②每一次换挡位,都要重新进行一次“欧姆调零”;
③在外电路,电流是从黑表笔流经被测电阻到红表笔的.
④测量时,若指针偏转很小(靠近∞附近),应换倍率较小的挡位再测.( )
| A. | ①③④ | B. | ①②③ | C. | ①②③④ | D. | ②④ |
 如图所示,光滑绝缘细管与水平面成30°角,在管的右上方P点固定一个点电荷+Q,P点与细管在同一竖直平面内,管的顶端A与P点连线水平,图中PB垂直AC,B是AC的中点.带电荷量为-q的小球(小球直径略小于细管的内径)从管中A处由静止开始沿管向下运动,AC长为l,它在A处时的加速度为a,不考虑小球电荷量对+Q形成的电场的影响.则在电场中( )
如图所示,光滑绝缘细管与水平面成30°角,在管的右上方P点固定一个点电荷+Q,P点与细管在同一竖直平面内,管的顶端A与P点连线水平,图中PB垂直AC,B是AC的中点.带电荷量为-q的小球(小球直径略小于细管的内径)从管中A处由静止开始沿管向下运动,AC长为l,它在A处时的加速度为a,不考虑小球电荷量对+Q形成的电场的影响.则在电场中( )| A. | B点的电势高于C点的电势 | B. | B点的电场强度大小是A点的2倍 | ||
| C. | 小球运动到C处的加速度为$\frac{g}{2}$-a | D. | 小球从A到C的过程中动能增加$\frac{mgl}{2}$ |
| A. | 同一时刻它们的加速度的大小一定相等 | |
| B. | 它们都做匀加速运动 | |
| C. | 静电力对它们都做正功 | |
| D. | 电势能减小 |
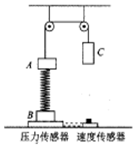 某同学利用图示装置来研究机械能守恒问题,设计了如下实验.
某同学利用图示装置来研究机械能守恒问题,设计了如下实验.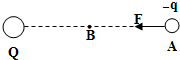 把一检验电荷q放在点电荷Q所形成的电场中的A点,若检验电荷的电量为q=-2.0×10-8C,它所受的电场力F=4.0×10-3N,方向指向Q,如图所示,A点到Q的距离为r=0.30m,已知静电常量K=9×109N•m2/C2,试求:
把一检验电荷q放在点电荷Q所形成的电场中的A点,若检验电荷的电量为q=-2.0×10-8C,它所受的电场力F=4.0×10-3N,方向指向Q,如图所示,A点到Q的距离为r=0.30m,已知静电常量K=9×109N•m2/C2,试求:
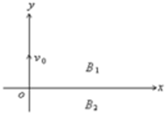 地球周围有磁场,由太空射来的带电粒子在此磁场中的运动称为磁漂移.以下描述的是一种假设的磁漂移运动.一带正电的粒子在x=0、y=0处沿y方向以某一速度v0运动,空间存在垂直于图中纸面向外的匀强磁场,在y>0的区域中,磁感强度为B1,在y<0的区域中磁感强度为B2,B2>B1,如图所示.
地球周围有磁场,由太空射来的带电粒子在此磁场中的运动称为磁漂移.以下描述的是一种假设的磁漂移运动.一带正电的粒子在x=0、y=0处沿y方向以某一速度v0运动,空间存在垂直于图中纸面向外的匀强磁场,在y>0的区域中,磁感强度为B1,在y<0的区域中磁感强度为B2,B2>B1,如图所示.