题目内容
12.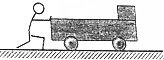 如图所示,质量为m1=10kg的方形箱子放在质量为m2=50kg的平板小车的上表面,两者右侧对齐,静止于水平地面.箱子与平板车上表面间的动摩擦因数μ=0.1,平板车与水平地面间的摩擦不计.一个人用向右的水平力推车,由于用力过大使箱子与车发生了相对滑动,人反应过来后撤去推力,这时推力已经作用了1s的时间.又经过一段时间箱子刚好滑到平板车的左侧边缘处.已知箱子边长d=0.2m,推力作用过程中,推力的平均值F=120N.取重力加速度g=10m/s2,求:
如图所示,质量为m1=10kg的方形箱子放在质量为m2=50kg的平板小车的上表面,两者右侧对齐,静止于水平地面.箱子与平板车上表面间的动摩擦因数μ=0.1,平板车与水平地面间的摩擦不计.一个人用向右的水平力推车,由于用力过大使箱子与车发生了相对滑动,人反应过来后撤去推力,这时推力已经作用了1s的时间.又经过一段时间箱子刚好滑到平板车的左侧边缘处.已知箱子边长d=0.2m,推力作用过程中,推力的平均值F=120N.取重力加速度g=10m/s2,求:(1)1s末木箱的速度v1及板车的速度v2;
(2)板车上表面的长度L.
分析 (1)箱子与车发生了相对滑动的过程中,根据牛顿第二定律分别求出两者的加速度,再根据速度时间公式求解1s末的速度;
(2)先根据位移时间公式求出1s内木箱相对小车的位移,撤去拉力后,木箱在滑动摩擦力作用下做匀加速直线运动,小车在滑动摩擦力作用下做匀加速直线运动,当两者速度相对时一起做匀速运动,根据运动学基本公式求出此过程中木箱相对小车向左运动的位移,最后求出小车的长度.
解答 解:(1)箱子与车发生了相对滑动的过程中,根据牛顿第二定律得:
木箱的加速度${a}_{1}=\frac{μ{m}_{1}g}{{m}_{1}}=1m/{s}^{2}$,
小车的加速度${a}_{2}=\frac{F-μ{m}_{1}g}{{m}_{2}}=\frac{120-0.1×10×10}{50}=2.2m/{s}^{2}$,
则1s末木箱的速度v1=a1t=1m/s,
小车的速度v2=a2t=2.2m/s,
(2)1s内木箱相对小车的位移${x}_{1}=\frac{1}{2}{a}_{2}{t}^{2}-\frac{1}{2}{a}_{1}{t}^{2}=\frac{1}{2}×2.2×1-\frac{1}{2}×1×1$=0.6m,
撤去拉力后,木箱在滑动摩擦力作用下做匀加速直线运动,小车在滑动摩擦力作用下做匀加速直线运动,当两者速度相对时一起做匀速运动,
此过程中,木箱的加速度不变,小车的加速度${a}_{3}=\frac{-μ{m}_{1}g}{{m}_{2}}=-0.2m/{s}^{2}$,
设经过时间t1木箱和小车的速度相等,则有:
v1+a1t1=v2+a3t1
解得:t1=1s
共同速度v=v1+a1t1=1+1=2m/s
此过程中,木箱相对小车向左运动的位移x2=$\frac{{v}_{2}+v}{2}{t}_{1}-\frac{{v}_{1}+v}{2}{t}_{1}$=0.6m,
则小车的长度L=x1+x2+d=0.6+0.6+0.2=1.4m.
答:(1)1s末木箱的速度v1为1m/s,板车的速度v2为2.2m/s;
(2)板车上表面的长度L为1.4m.
点评 本题主要考查了牛顿第二定律和运动学基本公式的直接应用,要求同学们能正确分析物体的受力情况和运动情况,特别注意木箱本身有一定的长度,难度适中.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | 牛顿第一定律是经过多次的实验验证而得出的 | |
| B. | 牛顿第三定律和第一、第二定律共同组成了牛顿运动定律,阐述了经典力学中基本的运动规律 | |
| C. | 牛顿提出万有引力定律并据此计算出了地球的质量 | |
| D. | 牛顿第一定律只是牛顿第二定律的一个特例 |
| A. | 子弹射出枪口时的速度为800 m/s | |
| B. | 一辆公共汽车从甲站行驶到乙站,全过程的速度为40 km/h | |
| C. | 某段高速公路限速为90 km/h | |
| D. | 小球在第3s末的速度为6 m/s |
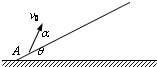
 如图所示,质量相同的A、B两个小球位于同一高度处,A球以v0竖直下抛,B球以v0沿光滑斜面向下运动,下列关于A、B两球的说法中正确的是( )
如图所示,质量相同的A、B两个小球位于同一高度处,A球以v0竖直下抛,B球以v0沿光滑斜面向下运动,下列关于A、B两球的说法中正确的是( )| A. | 两球落地时速度相同 | |
| B. | 两球落地时,A球重力的瞬时功率较小 | |
| C. | 从开始至落地,B球在相等的时间内速度的变化较大 | |
| D. | 从开始至落地,A球重力的平均功率较大 |

| A. | P、Q点的线速度大小相等 | |
| B. | P、Q点的角速度相等 | |
| C. | P点摩擦力方向与轮的转动方向相反,Q点的摩擦力方向与轮的转动方向相同 | |
| D. | P点摩擦力方向与轮的转动方向相同,Q点的摩擦力方向与轮的转动方向相反 |
 如图所示,传送带以v=4m/s的速率逆时针转动,在传送带的右侧无初速度的释放一个物体A(视为质点),已知两轴心间距离O1O2的长L=8m,物体与传送带间的动摩擦因素μ=0.2,求:
如图所示,传送带以v=4m/s的速率逆时针转动,在传送带的右侧无初速度的释放一个物体A(视为质点),已知两轴心间距离O1O2的长L=8m,物体与传送带间的动摩擦因素μ=0.2,求: 质量为m=2.0kg的物体原来静止在水平面上的A处,在F=15N水平恒力作用下运动L=10m时速度达到v=10m/s,然后立即将力F大小不变,方向改为与水平方向成53°,斜向下的推力,如图所示,g=10m/s2,sin53°=0.8,cos53°=0.6.
质量为m=2.0kg的物体原来静止在水平面上的A处,在F=15N水平恒力作用下运动L=10m时速度达到v=10m/s,然后立即将力F大小不变,方向改为与水平方向成53°,斜向下的推力,如图所示,g=10m/s2,sin53°=0.8,cos53°=0.6.