题目内容
12. 如图所示,一平直的传送带以速率v0匀速运行,把一工件从A处运送到B处,A、B相距d,工件与传送带间的动摩擦因数μ.若从A处把工件轻轻放到传送带上,那么工件从A到B所用时间可能为( )
如图所示,一平直的传送带以速率v0匀速运行,把一工件从A处运送到B处,A、B相距d,工件与传送带间的动摩擦因数μ.若从A处把工件轻轻放到传送带上,那么工件从A到B所用时间可能为( )| A. | $\sqrt{\frac{2d}{μg}}$ | B. | $\frac{2d}{{v}_{0}}$ | C. | $\frac{d}{{v}_{0}}$ | D. | $\frac{d}{{v}_{0}}$+$\frac{{v}_{0}}{2μg}$ |
分析 在A处把工件轻轻放到传送带上,工件受到滑动摩擦力而做加速运动,传送带足够长,工件可能先匀加速后匀速,若传送带较短,工件可能一直匀加速,由牛顿第二定律和速度时间公式求出工件一直匀加速的时间,再进行选择.
解答 解:A、工件在传送带上匀加速运动时的加速度为 a=$\frac{μmg}{m}$=μg
若工件一直做匀加速运动,则有 d=$\frac{1}{2}a{t}^{2}$,得 t=$\sqrt{\frac{2d}{μg}}$,故A正确.
B、若工件一直做匀加速运动,到达B点时速度恰好等于传送带速度v0时,则有 d=$\frac{{v}_{0}}{2}t$,得 t=$\frac{2d}{{v}_{0}}$,故B正确.
CD、若工件先匀加速运动,后匀速运动,则
工件匀加速至速度等于传送带速度时所用时间 t1=$\frac{{v}_{0}}{a}$=$\frac{{v}_{0}}{μg}$
通过的位移为 x1=$\frac{{v}_{0}}{2}{t}_{1}$=$\frac{{v}_{0}^{2}}{2μg}$
匀速运动的时间为 t2=$\frac{d-{x}_{1}}{{v}_{0}}$=$\frac{d}{{v}_{0}}$-$\frac{{v}_{0}}{2μg}$
总时间为 t=t1+t2=$\frac{d}{{v}_{0}}$+$\frac{{v}_{0}}{2μg}$>$\frac{d}{{v}_{0}}$,故C错误,D正确.
故选:ABD
点评 在传送带问题中,工件是否能够达到与传送带相同的速度是解题的关键,要考虑各种可能的情况,不能漏解.

练习册系列答案
相关题目
16.某高铁行驶速度是300km/h,坐在此动车里的乘客认为自己是静止的,他所选择的参考系是( )
| A. | 地面 | B. | 坐在他身边的乘客 | ||
| C. | 铁路边的树木 | D. | 窗外的山峰 |
7.一水平面上的物体在水平恒力F作用下由静止开始运动了t秒,t秒末撤去该力,物体又经过3t秒停止运动,设撤掉F前后的加速度大小分别为a1和a2,物体在水平面上的摩擦力为Ff,则( )
| A. | a1:a2=1:3 | B. | a1:a2=3:1 | C. | Ff:F=1:3 | D. | Ff:F=1:4 |
17. 如图所示,在倾角为30°的光滑斜面上端系有一劲度系数为k=200N/m的轻质弹簧,弹簧下端连一个质量为m=2kg的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以a=6m/s2的加速度沿斜面向下做匀加速直线运动,斜面固定不动,取g=10m/s2,则( )
如图所示,在倾角为30°的光滑斜面上端系有一劲度系数为k=200N/m的轻质弹簧,弹簧下端连一个质量为m=2kg的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以a=6m/s2的加速度沿斜面向下做匀加速直线运动,斜面固定不动,取g=10m/s2,则( )
 如图所示,在倾角为30°的光滑斜面上端系有一劲度系数为k=200N/m的轻质弹簧,弹簧下端连一个质量为m=2kg的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以a=6m/s2的加速度沿斜面向下做匀加速直线运动,斜面固定不动,取g=10m/s2,则( )
如图所示,在倾角为30°的光滑斜面上端系有一劲度系数为k=200N/m的轻质弹簧,弹簧下端连一个质量为m=2kg的小球,球被一垂直于斜面的挡板A挡住,此时弹簧没有形变.若挡板A以a=6m/s2的加速度沿斜面向下做匀加速直线运动,斜面固定不动,取g=10m/s2,则( )| A. | 小球向下运动0.05 m时速度最大 | B. | 小球向下运动0.01 m时与挡板分离 | ||
| C. | 小球速度最大时与挡板分离 | D. | 小球从一开始运动就与挡板分离 |
2.穿过闭合回路的磁通量φ随时间t变化的图象分别如图①~④所示,下列关于回路中产生的感应电动势的论述,正确的是( )


| A. | 图①中回路产生的感应电动势恒定不变 | |
| B. | 图②中回路产生的感应电动势一直在变大 | |
| C. | 图③中回路在0~t1时间内产生的感应电动势是t1-t2时间内产生的感应电动势的2倍 | |
| D. | 图④中回路产生的感应电动势先变小再变大 |
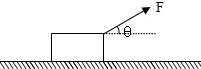 如图所示,质量为m=2kg的物体与水平地面的动摩擦因素为μ=0.2,现对物体施加一大小为10N,方向与水平方向成θ=37°角斜向上的力F,使之向右做匀加速直线运动,求:
如图所示,质量为m=2kg的物体与水平地面的动摩擦因素为μ=0.2,现对物体施加一大小为10N,方向与水平方向成θ=37°角斜向上的力F,使之向右做匀加速直线运动,求: 如图所示,水平传送带AB长为16m,传送带以4.0m/s的速度匀速运动.现在A处轻放一质量为m的小物体,已知物体与传送带之间的动摩擦因数为0.2(g=10m/s2).求:
如图所示,水平传送带AB长为16m,传送带以4.0m/s的速度匀速运动.现在A处轻放一质量为m的小物体,已知物体与传送带之间的动摩擦因数为0.2(g=10m/s2).求: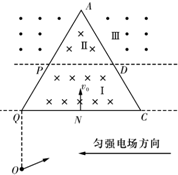 为了使粒子经过一系列的运动后,又以原来的速率沿相反方向回到原位,可设计如下的一个电磁场区域(如图所示):水平线QC以下是水平向左的匀强电场,区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场,磁感应强度为B;区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同,区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反.已知等边三角形AQC的边长为2L,P、D分别为AQ、AC的中点.带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出,在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ,再从P点垂直AQ射入区域Ⅲ,又经历一系列运动后返回O点.(粒子重力忽略不计)求:
为了使粒子经过一系列的运动后,又以原来的速率沿相反方向回到原位,可设计如下的一个电磁场区域(如图所示):水平线QC以下是水平向左的匀强电场,区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场,磁感应强度为B;区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同,区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反.已知等边三角形AQC的边长为2L,P、D分别为AQ、AC的中点.带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出,在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ,再从P点垂直AQ射入区域Ⅲ,又经历一系列运动后返回O点.(粒子重力忽略不计)求: