题目内容
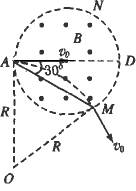
如图所示，在直径为d的圆形区域内有匀强磁场，磁场方向垂直于纸面．已知∠MAD＝∠NAD＝30°，有一个不计重力的质量为m、带电荷量为q的正电荷以v0的速率从A点沿直径AD方向射入磁场．求：
要使该粒子能打在MN弧上，磁感应强度B应满足什么条件？
答案：见详解
解析：
解析：
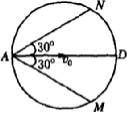
粒子打在D点，磁感应强度B应等于零． 粒子打在M点时，磁感应强度方向必须垂直纸面向外，粒子在洛伦兹力作用下沿AM弧做匀速圆周运动，如图下所示．
由几何关系知∠AOM＝60°，ΔAOM为等腰三角形 R＝dcos30°＝ 又因为R＝ 由式①和式②得B＝ 同理可得粒子打在N点时，磁感应强度方向必须垂直纸面向里．当B变大时，R变小，则可从MN弧上打出．因此，要使粒子能打在MN弧上，B必须满足：0≤B≤
|
d ①
②
．
练习册系列答案
相关题目
如图所示，在直径为D、电阻为R的细金属丝圆环区域内有一垂直于该圆环的变化磁场，其磁场的变化规律为B=B0+kt（k为大于零的常数），则以下说法正确的是（ ）| A、金属圆环中有顺时针方向的感应电流 | ||
B、金属圆环中通过的感应电流大小为
| ||
C、△t时间内，通过金属圆环横截面的电荷量为
| ||
D、△t时间内，金属圆环中产生的电热为
|
（k为大于零的常数），则以下说法正确的是（ ）
时间内，通过金属圆环横截面电荷量为
如图所示，在直径为D、匝数为N的圆形线圈中存在着随时间变化的匀强磁场，磁感应强度与时间的关系为
。线圈的总电阻为r，外接电阻R,其他电阻不计。则
A．通过电阻R的是交变电
B．通过电阻R的是恒定电流
|
D．通过电阻R的电流瞬时值表达式为
