题目内容
4.如图甲所示,竖直平面内有四条水平虚线L1、L2、L3、L4,间距分别为d、2d、3d,d=1.25m,L1和L2之间,L3和L4之间存在匀强磁场,磁感应强度大小相等,B=1T,方向垂直于纸面向内.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2.5QUOTE,将其从图示位置(cd边水平)由静止释放,cd边穿入L1开始计时,直至ab边离开L4,画出线框的v-t图如图乙所示,t1时刻cd与L2重合,t3时刻ab边恰好从L4离开磁场,t2-t3之间图线为与t轴平行的直线,t1-t2之间及t3之后为斜率相同的倾斜直线,整个运动过程中线圈始终位于竖直平面内.(重力加速度g取10m/s2),则( )
| A. | t2时刻,ab边恰好经过L1 | B. | 线圈匀速运动时速度大小v2=10m/s | ||
| C. | t2-t3之间的时间间隔为0.75s | D. | t2-t3之间产生的热量为6.25J |
分析 根据t2-t3内线框匀速运动,可分析出bc边长,即判断t2时刻ab边的位置.根据平衡条件求线圈匀速运动时速度.由匀速运动的位移规律求t2-t3之间的时间间隔.由能量守恒求热量.
解答 解:A、由图乙知,t2-t3内线框匀速运动,t2时刻在L3下方d处,t3时刻ab边恰好从L4离开磁场,说明bc=3d.则t2时刻,ab边恰好经过L2.故A错误.
B、线圈匀速运动时,有mg=$\frac{{B}^{2}{L}^{2}{v}_{2}}{R}$,得v2=$\frac{mgR}{{B}^{2}{L}^{2}}$=$\frac{1×2.5}{{1}^{2}×0.{5}^{2}}$=10m/s,故B正确.
C、t2-t3之间内线框下落的距离为5d,则t2-t3之间的时间间隔为 t=$\frac{5d}{{v}_{2}}$=0.625s,故C错误.
D、t2-t3之间产生的热量为 Q=mg•5d=0.1×10×5×1.25J=6.25J.故D正确.
故选:BD.
点评 解决本题的关键理清线圈的运动情况,选择合适的规律进行求解,本题的难点就是通过线圈匀速直线运动挖掘出线框下落的位移为3d.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
15. 卢瑟福通过α粒子散射实验,判断出原子的中心有一个很小的核,并由此提出了原子的核式结构.如图所示的示意图中,①、②两条线表示实验中α粒子运动的轨迹,则沿③所示方向射向原子核的α粒子可能的运动轨迹为( )
卢瑟福通过α粒子散射实验,判断出原子的中心有一个很小的核,并由此提出了原子的核式结构.如图所示的示意图中,①、②两条线表示实验中α粒子运动的轨迹,则沿③所示方向射向原子核的α粒子可能的运动轨迹为( )
 卢瑟福通过α粒子散射实验,判断出原子的中心有一个很小的核,并由此提出了原子的核式结构.如图所示的示意图中,①、②两条线表示实验中α粒子运动的轨迹,则沿③所示方向射向原子核的α粒子可能的运动轨迹为( )
卢瑟福通过α粒子散射实验,判断出原子的中心有一个很小的核,并由此提出了原子的核式结构.如图所示的示意图中,①、②两条线表示实验中α粒子运动的轨迹,则沿③所示方向射向原子核的α粒子可能的运动轨迹为( )| A. | 轨迹a | B. | 轨迹b | C. | 轨迹c | D. | 轨迹d |
16.一人造卫星在半径为R的轨道绕地球做匀速圆周运动,若该卫星在半径为2R的轨道上绕地球做匀速圆周运动,则( )
| A. | 卫星运动的线速度将增大到原来的2倍 | |
| B. | 卫星运动的线速度将减小到原来的$\frac{\sqrt{2}}{2}$ | |
| C. | 地球提供卫星的向心力将减小到原来的2倍 | |
| D. | 地球提供卫星的向心力将减小到原来的$\frac{1}{4}$ |
 生活中的碰撞事件极为常见:
生活中的碰撞事件极为常见: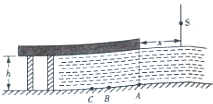 一湖面上有一伸向水面的混凝土观景台,如图所示是一截面图,观景台下表面恰好和水面相平,A为观景台右侧在湖底的投影,水深h=4m.在距观景台右侧面x=4m处有一可沿竖直方向上下移动的单色点光源S,点光源S可从距水面高3m处下移到接近水面,在移动过程中,观景台水下被照亮的最远距离为AC,最近距离为AB,若AB=3m,求:
一湖面上有一伸向水面的混凝土观景台,如图所示是一截面图,观景台下表面恰好和水面相平,A为观景台右侧在湖底的投影,水深h=4m.在距观景台右侧面x=4m处有一可沿竖直方向上下移动的单色点光源S,点光源S可从距水面高3m处下移到接近水面,在移动过程中,观景台水下被照亮的最远距离为AC,最近距离为AB,若AB=3m,求: 如图(a)所示,在真空中,半径为b的虚线所围的圆形区域内存在匀强磁场,磁场方向与纸面垂直.在磁场右侧有一对平行金属板M和N,两板间距离也为b,板长为2b,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上.有一电荷量为+q、质量为m的带电粒子,以速率v0从圆周上的P点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如图(b)所示电压u.最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力.
如图(a)所示,在真空中,半径为b的虚线所围的圆形区域内存在匀强磁场,磁场方向与纸面垂直.在磁场右侧有一对平行金属板M和N,两板间距离也为b,板长为2b,两板的中心线O1O2与磁场区域的圆心O在同一直线上,两板左端与O1也在同一直线上.有一电荷量为+q、质量为m的带电粒子,以速率v0从圆周上的P点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点飞出磁场时,给M、N板加上如图(b)所示电压u.最后粒子刚好以平行于N板的速度,从N板的边缘飞出.不计平行金属板两端的边缘效应及粒子所受的重力. 如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求: