题目内容
9. 如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,光滑圆弧BC与水平面和传送带分别相切于B,C两点,圆弧所对应的圆心角θ=37°,圆弧BC的半径R=7m,足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角也为θ,一质量m=1kg的小滑块从A点以大小v0=10m/s的初速度向B点运动,A,B间的距离s=3.6m,已知小滑块与水平面、传送带之间的动摩擦因数均为μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)小滑块第一次滑到C点时的速度的大小;
(2)小滑块到达最高点时,相对C点增加的重力势能;
(3)小滑块到达最高点时,小滑块与传送带间由于摩擦而产生的热量.
分析 (1)A到C的过程中重力与摩擦力做功,根据动能定理即可求得物体第一次到达C的速度.
(2)由于物体在传送带上时,重力沿斜面向下的分力大于摩擦力,所以物体在传送带上的减速运动分成两个阶段,对物体分别进行受力分析,求得两个阶段的加速度,然后根据运动学的公式分别求出两个阶段的位移大小,从而求得物块上升的最大高度,即可求得增加的重力势能.
(3)由功的计算公式可以求出滑块与传送带间因摩擦产生的热量.
解答 解:(1)C离A的高度:h=R-Rcosθ=R-0.8R=0.2R=1.4m
滑块从A到C的过程中,由动能定理得:
-mgh-μmgs=$\frac{1}{2}$mvc2-$\frac{1}{2}$mv02,
代入数据解得:vc=6m/s;
(2)物体在传送带上运动的加速度大小为a1,则:
a1=gsinθ+μgcosθ=10×sin37°+0.5×10×cos37°=10m/s 2,
设物体在传送带上达到与传送带等速时的时间为t1,则:
v=vc-a1t1,解得:t1=$\frac{{v}_{C}-v}{{a}_{1}}$=$\frac{6-4}{10}$s=0.2s.
向上的位移:x1=$\frac{{v}_{C}+v}{2}$t1=$\frac{6+4}{2}$×0.2=1m,
由于 mgsinθ>μmgcosθ
物体继续在传送带上减速上滑,加速度大小为:
a2=gsinθ-μgcosθ=10×sin37°-0.5×10×cos37°=2m/s2
继续向上滑动的时间:t2=$\frac{v}{{a}_{2}}$=$\frac{4}{2}$=2s,
继续向上滑动的位移:x2=$\frac{v}{2}$t2=$\frac{4}{2}$×2=4m,
向上运动的最大距离:x=x1+x2=1m+4m=5m.
小滑块到达的最高点时,相对C点增加的重力势能增加量为:△EP=mgxsin30°=30J;
(3)小滑块与传送带间由于摩擦产生的热量:
Q=W=fx=μmgxcosθ=0.5×1×10×5cos37°=20J;
答:(1)小滑块第一次滑到C点时的速度大小为6m/s;
(2)小滑块到达的最高点时,相对C点增加的重力势能为30J;
(3)小滑块到达最高点时,小滑块与传送带间由于摩擦而产生的热量为20J.
点评 解决本题的关键理清物体的运动过程,知道物体的运动规律,结合动能定理、牛顿第二定律和运动学公式进行求解.

 阅读快车系列答案
阅读快车系列答案| A. | 无论光强多强,只要光的频率小于极限频率就不能产生光电效应 | |
| B. | 无论光的频率多低,只要光照时间足够长就能产生光电效应 | |
| C. | 超过极限频率的入射光频率越大,所产生的光电子的最大初动能就越大 | |
| D. | 发生光电效应所产生的光电子最大初动能,与入射光的频率成正比 |
 如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )| A. | 3.6cm/s | B. | 4.8cm/s | C. | 6 cm/s | D. | 7.2 cm/s |

| A. | t2时刻,ab边恰好经过L1 | B. | 线圈匀速运动时速度大小v2=10m/s | ||
| C. | t2-t3之间的时间间隔为0.75s | D. | t2-t3之间产生的热量为6.25J |
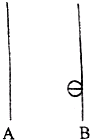 如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.
如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.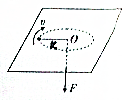 如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径R做匀速圆周运动,现开始缓慢地减小拉力,当拉力变为原来的四分之一时,小球仍做匀速圆周运动,半径变为2R,计算此过程中拉力对小球做的功.
如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径R做匀速圆周运动,现开始缓慢地减小拉力,当拉力变为原来的四分之一时,小球仍做匀速圆周运动,半径变为2R,计算此过程中拉力对小球做的功.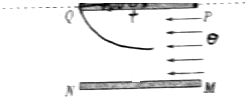 MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$.
MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$. 如图是一个多用表欧姆挡内部电路示意图.电流表满偏电流0.5mA、内阻10Ω;电池电动势1.5V、内阻1Ω;变阻器R0阻值0-5000Ω.
如图是一个多用表欧姆挡内部电路示意图.电流表满偏电流0.5mA、内阻10Ω;电池电动势1.5V、内阻1Ω;变阻器R0阻值0-5000Ω.