题目内容
12.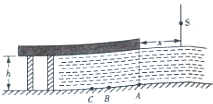 一湖面上有一伸向水面的混凝土观景台,如图所示是一截面图,观景台下表面恰好和水面相平,A为观景台右侧在湖底的投影,水深h=4m.在距观景台右侧面x=4m处有一可沿竖直方向上下移动的单色点光源S,点光源S可从距水面高3m处下移到接近水面,在移动过程中,观景台水下被照亮的最远距离为AC,最近距离为AB,若AB=3m,求:
一湖面上有一伸向水面的混凝土观景台,如图所示是一截面图,观景台下表面恰好和水面相平,A为观景台右侧在湖底的投影,水深h=4m.在距观景台右侧面x=4m处有一可沿竖直方向上下移动的单色点光源S,点光源S可从距水面高3m处下移到接近水面,在移动过程中,观景台水下被照亮的最远距离为AC,最近距离为AB,若AB=3m,求:(i)水的折射率n;
(ii)光能照亮的最远距离AC(计算结果可以保留根号)
分析 (i)据题,观景台水下被照亮的最近距离为AB,光线在水面发生了折射,由数学知识求入射角与折射角的正弦值,即可求得折射率.
(ii)点光源S接近水面时,入射角为90°,光能照亮的距离最远,由折射定律求出折射角,即可由几何知识求解最远距离AC.
解答 解:(i)点光源S在距水面高3m处发出的光在观景台右侧面与水面交接处折射到水里时,被照亮的距离为最近距离AB,则:
由于n=$\frac{sini}{sinr}$
所以:水的折射率 n=$\frac{\frac{x}{\sqrt{{x}^{2}+{3}^{2}}}}{\frac{AB}{\sqrt{A{B}^{2}+{h}^{2}}}}$=$\frac{4}{3}$
②点光源S接近水面时,光在观景台右侧面与水面交接处掠射到水里时,被照亮的距离为最远距离AC,此时,入射角为90°,折射角为临界角C,
则:n=$\frac{1}{sinC}$=$\frac{\sqrt{A{C}^{2}+{h}^{2}}}{AC}$=$\frac{4}{3}$
解得:AC=$\frac{12}{7}\sqrt{7}$≈4.5m
答:
(ⅰ)水的折射率n为$\frac{4}{3}$;
(ⅱ)光能照亮的最远距离AC为4.5m
点评 本题以折射率和全反射为命题背景考查学生的推理能力和分析综合能力,关键能运用数学知识求解入射角和折射角的正弦值,知道入射角最大时折射角也最大.

练习册系列答案
相关题目
3.在物理研究方法中,研究图象的面积可以得到相应的物理量,在下列物理量函数关系图象中,通过研究面积可得到对应物理量的是( )
| A. | 由I-t图线和横轴围成的面积可得到对应时间内通过导体横截面积的电荷量 | |
| B. | 由F-v图线和横轴围成的面积可得到对应速度变化过程中的总功率 | |
| C. | 由F-t图线和横轴围成的面积可得到对应时间内力对物体所做的功 | |
| D. | 由u-I图线和横轴围成的面积可得到对应的电功率 |
20. 如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
 如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )
如图为一横波发生器的显示屏,可以显示出波由0点从左向右传播的图象,屏上每一小格长度为1cm,在t=0时刻横波发生器上能显示的波形如图所示.因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5秒时,观察者看到C处恰好第三次(从C开始振动后算起)出现平衡位置,则该波的波速可能是( )| A. | 3.6cm/s | B. | 4.8cm/s | C. | 6 cm/s | D. | 7.2 cm/s |
7. 如图所示,两根轻绳一端系于结点O,另一端分别系于固定环上的A、B两点,O点下面悬挂一物体M,绳OA水平,拉力大小为F1,绳OB与OA夹角α=120°,拉力大小为F2.将两绳同时缓慢顺时针转过75°,并保持两绳之间的夹角α始终不变,且物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )
如图所示,两根轻绳一端系于结点O,另一端分别系于固定环上的A、B两点,O点下面悬挂一物体M,绳OA水平,拉力大小为F1,绳OB与OA夹角α=120°,拉力大小为F2.将两绳同时缓慢顺时针转过75°,并保持两绳之间的夹角α始终不变,且物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )
 如图所示,两根轻绳一端系于结点O,另一端分别系于固定环上的A、B两点,O点下面悬挂一物体M,绳OA水平,拉力大小为F1,绳OB与OA夹角α=120°,拉力大小为F2.将两绳同时缓慢顺时针转过75°,并保持两绳之间的夹角α始终不变,且物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )
如图所示,两根轻绳一端系于结点O,另一端分别系于固定环上的A、B两点,O点下面悬挂一物体M,绳OA水平,拉力大小为F1,绳OB与OA夹角α=120°,拉力大小为F2.将两绳同时缓慢顺时针转过75°,并保持两绳之间的夹角α始终不变,且物体始终保持静止状态.则在旋转过程中,下列说法正确的是( )| A. | F1逐渐增大 | B. | F1先增大后减小 | C. | F2逐渐减小 | D. | F2先减小后增大 |
4.如图甲所示,竖直平面内有四条水平虚线L1、L2、L3、L4,间距分别为d、2d、3d,d=1.25m,L1和L2之间,L3和L4之间存在匀强磁场,磁感应强度大小相等,B=1T,方向垂直于纸面向内.现有一矩形线圈abcd,宽度cd=L=0.5m,质量为0.1kg,电阻为2.5QUOTE,将其从图示位置(cd边水平)由静止释放,cd边穿入L1开始计时,直至ab边离开L4,画出线框的v-t图如图乙所示,t1时刻cd与L2重合,t3时刻ab边恰好从L4离开磁场,t2-t3之间图线为与t轴平行的直线,t1-t2之间及t3之后为斜率相同的倾斜直线,整个运动过程中线圈始终位于竖直平面内.(重力加速度g取10m/s2),则( )

| A. | t2时刻,ab边恰好经过L1 | B. | 线圈匀速运动时速度大小v2=10m/s | ||
| C. | t2-t3之间的时间间隔为0.75s | D. | t2-t3之间产生的热量为6.25J |
2.两个正、负点电荷周围电场线分布如图所示,P、Q为电场中两点,则( )


| A. | 正电荷由P静止释放能运动到Q | |
| B. | 正电荷在P的加速度小于在Q的加速度 | |
| C. | 负电荷在P的电势能高于在Q的电势能 | |
| D. | 负电荷从P移动到Q,其间必有一点电势能为零 |
 某同学根据平抛运动规律设计“粗测玩具手枪弹丸的发射速度v0”的实验方案,实验示意图如图所示,弹丸初速度水平(没有计时仪器).
某同学根据平抛运动规律设计“粗测玩具手枪弹丸的发射速度v0”的实验方案,实验示意图如图所示,弹丸初速度水平(没有计时仪器).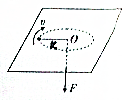 如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径R做匀速圆周运动,现开始缓慢地减小拉力,当拉力变为原来的四分之一时,小球仍做匀速圆周运动,半径变为2R,计算此过程中拉力对小球做的功.
如图所示,在一块水平放置的光滑板中心开一个小孔,穿过一根细绳,细绳的一端用力F向下拉,另一端系一小球,使小球在板面上以半径R做匀速圆周运动,现开始缓慢地减小拉力,当拉力变为原来的四分之一时,小球仍做匀速圆周运动,半径变为2R,计算此过程中拉力对小球做的功.