题目内容
16. 如图为竖直放置的绝缘轨道,中心放一带电量为+Q的点电荷,轨道的半径为r,质量为m、带电量为-q的绝缘带电小球(可视为质点)从最低点A点以一定的初速度向右运动.
如图为竖直放置的绝缘轨道,中心放一带电量为+Q的点电荷,轨道的半径为r,质量为m、带电量为-q的绝缘带电小球(可视为质点)从最低点A点以一定的初速度向右运动.(1)若不计小球所受的阻力,且小球恰能过B点,求小球通过A点时速度vA的大小.
(2)若小球所受阻力不可忽略,且小球在A点与B点的压力大小之差为△F,求小球从A点运动到B点的过程所受阻力做的功.
分析 (1)在B点由牛顿第二定律求的B点的最小速度,从A到B由动能定理即可求得A点速度;
(2)在AB两点由牛顿第二定律求的小球在A点与B点的压力大小,由动能定理即可求得
解答 解:(1)在最高点由牛顿第二定律得$mg+\frac{kqQ}{{r}^{2}}=\frac{m{v}^{2}}{r}$
从A到B由动能定理可知$-2mgr=\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{A}^{2}$
联立解得${v}_{A}=\sqrt{5gr+\frac{kqQ}{mr}}$
(2)在A点,${F}_{N1}+\frac{kQq}{{r}^{2}}-mg=\frac{{mv}_{1}^{2}}{r}$
在B点$mg+\frac{kQq}{{r}^{2}}-{F}_{N}=\frac{{mv}_{2}^{2}}{r}$
从A到B由动能定理可知
-2mgr-Wf=$\frac{1}{2}{mv}_{2}^{2}-\frac{1}{2}{mv}_{1}^{2}$
△F=FN1-FN
联立解得Wf=△Fr-2mgr
答:(1)若不计小球所受的阻力,且小球恰能过B点,小球通过A点时速度vA的大小$\sqrt{5gr+\frac{kqQ}{mr}}$.
(2)若小球所受阻力不可忽略,且小球在A点与B点的压力大小之差为△F,小球从A点运动到B点的过程所受阻力做的功为△Fr-2mgr.
点评 本题主要考查了动能定理的应用,抓住过程利用好动能定理即可

练习册系列答案
相关题目
10. 如图所示,B、C、D三点都在以点电荷+Q为圆心、半径为r的圆弧上,将一试探电荷从A点分别移到B、C、D各点时,静电力做功的关系( )
如图所示,B、C、D三点都在以点电荷+Q为圆心、半径为r的圆弧上,将一试探电荷从A点分别移到B、C、D各点时,静电力做功的关系( )
 如图所示,B、C、D三点都在以点电荷+Q为圆心、半径为r的圆弧上,将一试探电荷从A点分别移到B、C、D各点时,静电力做功的关系( )
如图所示,B、C、D三点都在以点电荷+Q为圆心、半径为r的圆弧上,将一试探电荷从A点分别移到B、C、D各点时,静电力做功的关系( )| A. | WAB>WAC | B. | WAB=WAC | C. | WAD>WAB | D. | WAC>WAD |
11.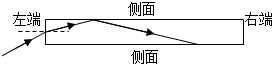 如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )
如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )
 如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )
如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )| A. | 增加单色光的频率,光在光纤中的传播速度将增大 | |
| B. | 改变光在左端面的入射角,光在光纤中的传播时间不变 | |
| C. | 该单色光在光纤中传播的最短时间为$\frac{nL}{c}$ | |
| D. | n$<\sqrt{2}$ |
1.下列说法正确的是( )
| A. | 光电效应既显示了光的粒子性,又显示了光的波动性 | |
| B. | 原子核内的中子转化成一个质子和一个电子,这种转化产生的电子发射到核外,就是β粒子,这就是β衰变的实质 | |
| C. | 一个氘核${\;}_{1}^{2}$H与一个氚核${\;}_{1}^{3}$H聚变生成一个氦核${\;}_{2}^{4}$He的同时,放出一个质子 | |
| D. | 光子的能量由光的频率所决定 | |
| E. | 按照玻尔理论,氢原子核外从半径较小的轨道跃迁半径较大的轨道时,电子的动能减小,电势能增大,原子的总能量增大 |
8. 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )| A. | 由此可知d电势高于c电势 | |
| B. | 由此可知Ⅰ是S极 | |
| C. | 由此可知Ⅰ是N极 | |
| D. | 当cd棒向下运动时,ab导线受到向左的磁场力 |
5.已知地球的半径为R,地球表面的重力加速度为g,环绕地球运行的一颗人造地球卫星的线速度为v,则下列说法正确的是( )
| A. | 地球的第一宇宙速度小于v | B. | 该卫星的轨道半径为$\frac{{v}^{2}}{g{R}^{2}}$ | ||
| C. | 该卫星的运行周期为2π$\frac{{gR}^{2}}{{v}^{3}}$ | D. | 该卫星的向心加速度为$\frac{{v}^{2}}{g{R}^{2}}$ |
6.关于行星绕太阳运动,下列说法正确的是( )
| A. | 行星在椭圆轨道上绕太阳运动的过程中,其速度随行星与太阳之间距离的变化而变化,距离小时速度小,距离大时速度大 | |
| B. | 开普勒第三定律中定值K与行星的质量无关,只与太阳的质量有关 | |
| C. | 所有行星绕太阳运动的周期是相等的 | |
| D. | 行星在椭圆轨道上绕太阳运动的过程中,太阳在所有行星运动轨道的一个焦点上 |
 如图所示的装置为一个光滑圆弧轨道与水平轨道相连,小物块A、B质量均为m,水平轨道上PQ段长为l与小物块间的动摩擦因数为μ,其余段光滑.初始时,轻质弹簧处于原长,其左端带有轻质挡板静止于Q点,轻质弹簧右端固定在O点;小物块A从光滑圆弧轨道上高为h处无初速度滑下,与静止在光滑圆弧轨道末端的B发生完全非弹性碰撞,之后A、B一起向右运动,不再返回P点左侧.
如图所示的装置为一个光滑圆弧轨道与水平轨道相连,小物块A、B质量均为m,水平轨道上PQ段长为l与小物块间的动摩擦因数为μ,其余段光滑.初始时,轻质弹簧处于原长,其左端带有轻质挡板静止于Q点,轻质弹簧右端固定在O点;小物块A从光滑圆弧轨道上高为h处无初速度滑下,与静止在光滑圆弧轨道末端的B发生完全非弹性碰撞,之后A、B一起向右运动,不再返回P点左侧. 如图所示,在直角坐标系XOY中,X轴上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向外.许多质量m、电荷量为+q的粒子,以相同的速率V沿纸面内,由X轴负方向与y轴正方向之间各个方向从原点O射入磁场区域.不计重力及粒子间的相互作用.下列图中阴影部分表示带电粒子在磁场中可能经过的区域,其中R=$\frac{mv}{qB}$,正确的图是( )
如图所示,在直角坐标系XOY中,X轴上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向外.许多质量m、电荷量为+q的粒子,以相同的速率V沿纸面内,由X轴负方向与y轴正方向之间各个方向从原点O射入磁场区域.不计重力及粒子间的相互作用.下列图中阴影部分表示带电粒子在磁场中可能经过的区域,其中R=$\frac{mv}{qB}$,正确的图是( )


