题目内容

16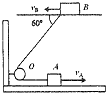．如图所示，有两条位于同一竖直平面内的水平轨道，轨道上有两个物体A和B，它们通过一根绕过定滑轮O的不可伸长的轻绳相连接，物体B以vB=10m/s匀速运动，在绳子与轨道α=60°角时，物体A的速度大小vA为：（　　）
A．5m/sB．5$\sqrt{3}$m/sC．20m/sD．10m/s

分析 根据运动的合成与分解，结合A的速度与B的速度沿着绳子方向的速度大小相等，结合平行四边形定则求出物体A的速度．

解答 解：将B点的速度分解如右图所示，则有：
v2=vA，v2=vBcos60°．
解得：vA=10×$\frac{1}{2}$=5m/s，故A正确，BCD错误；
故选：A．

点评 本题考查了运动的合成分解，知道小滑块沿着绳子的速度与A的速度大小相等，方向相．以及知道分运动与合运动具有等时性．

练习册系列答案
相关题目
18．关于曲线运动的叙述，正确的是（　　）
A．做曲线运动的物体，速度方向时刻变化，故曲线运动不可能是匀变速运动
B．物体在一恒力作用下不可能做曲线运动
C．做曲线运动的物体一定具有不为零的加速度
D．物体只有受到方向时刻变化的力的作用才可能做曲线运动
19．两个质量分别为2m和m的小木块a和b（可视为质点）放在水平圆盘上，a与转轴OO′的距离为L，b与转轴的距离为2L，a、b之间用长为L的强度足够大的轻绳相连，木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g．若圆盘从静止开始绕转轴缓慢地加速转动，开始时轻绳刚好伸直但无张力，用ω表示圆盘转动的角速度，下列说法正确的是（　　）
A．a比b先达到最大静摩擦力
B．a、b所受的摩擦力始终相等
C．ω=$\sqrt{\frac{kg}{2L}}$是b开始滑动的临界角速度
D．当ω=$\sqrt{\frac{2kg}{3L}}$时，a所受摩擦力的大小为$\frac{5kmg}{3}$
4．关于自由落体运动，下列说法正确的是（　　）
A．物体竖直向下的运动就称之为自由落体运动
B．自由落体运动的初速度一定为0
C．只要在重力作用下的物体下落的运动就是自由落体运动
D．阻力可以被忽略不计的运动称之为自由落体运动
11．如图所示，A、B为两只完好的相同灯泡，L是带有铁芯、电阻可不计的线圈，K为开关，下列说法中正确的是（　　）
A．K闭合瞬间，A、B两灯均立即变亮B．K闭合稳定后，A、B一直都亮着
C．K断开瞬间，A亮一下再熄灭D．K断开瞬间，A、B同时熄灭
1．水平恒力F作用于放在光滑水平面上质量为m的物体上，使m沿力的方向运动的位移为s，此时力F做功大小为W1；若使水平恒力F作用于放在粗糙水平面上的质量为2m的物体上，使其沿力的方向运动的位移也为s，此时F做功大小为W2，则比较W1与W2的大小为（　　）
A．W1＞W2B．W1=W2C．W1＜W2D．无法判断
8．如图所示，体重为60kg的武术运动员，两脚蹬在两堵墙上且保持静止状态，已知运动员的脚与墙面间的动摩擦因数均为0.5，两堵墙之间的距离和运动员的腿长相等．若滑动摩擦力等于静摩擦力最大值．则关于运动员与墙之间的压力大小正确的是（取g=10m/s2）（　　）
A．一定等于600NB．可能等于600N
C．一定大于等于1200ND．可能小于600N
5．为了演示接通电源的瞬间和断开电源的瞬间的电磁感应现象，设计了如图所示的电路图，A、B两灯规格相同，L的直流电阻和R相等，开关接通的瞬间，A灯的亮度大于（填“大于”“等于”或“小于”）B灯的亮度；通电一段时间后，A灯的两端等于（填“大于”“等于”或“小于”）B灯的亮度；断电的瞬间，B灯立即（填“立即”或“逐渐”）熄灭．
6．交流电的有效值是根据能量的等效计算出来的一个数值，以下是交流电有效值的有（　　）
A．交流电表的读数B．保险丝的熔断电流
C．电容器的击穿电压D．电器铭牌上的额定电压

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网