题目内容
19.木星是绕太阳公转的行星之一,而木星的周围又有卫星绕木星公转.如果要通过观测求得木星的质量M,已知万有引力常量为G,则需要测量的量及木星质量的计算式是( )| A. | 卫星的公转周期T1和轨道半径r1,$M=\frac{4{π}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$ | |
| B. | 卫星的公转周期T1和轨道半径r1,$M=\frac{G{T}_{1}^{2}}{4{π}^{2}{r}_{1}^{3}}$ | |
| C. | 木星的公转周期T2和轨道半径r2,$M=\frac{4{π}^{2}{r}_{2}^{3}}{G{T}_{2}^{2}}$ | |
| D. | 木星的公转周期T2和轨道半径r2,$M=\frac{G{T}_{2}^{2}}{4{π}^{2}{r}_{2}^{3}}$ |
分析 根据木星的某个卫星的万有引力等于向心力,列式求解即可求出木星的质量.
解答 解:环绕天体绕着中心天体做匀速圆周运动,根据牛顿第二定律,有:
G$\frac{Mm}{{R}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}R$
解得:
M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$
即只能求解中心天体的质量;
故要测量木星质量,需要测量其卫星的公转周期T1和轨道半径r1,故其质量为:
$M=\frac{4{π}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$
故A正确,BCD错误;
故选:A.
点评 本题关键是根据木星的卫星做圆周运动的向心力有万有引力提供,列出方程,分析方程式即可看出要测量的量,涉及半径有星体半径和轨道半径,解题时要注意区分.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 由玻尔理论可知,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能减小,电势能增大 | |
| B. | 对于同一种金属来说,其极限频率恒定,与入射光的频率及光的强度均无关 | |
| C. | 比结合能越大表示原子核中的核子结合得越牢固 | |
| D. | 通过α粒子散射实验可以估算原子核的大小 | |
| E. | 太阳内部发生的核反应是${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{144}$Ba+${\;}_{36}^{89}$Kr+3${\;}_{0}^{1}$n |
7.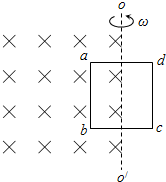 如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )
如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )
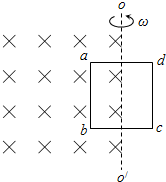 如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )
如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )| A. | $\frac{{\sqrt{2}Bsω}}{4R}$ | B. | $\frac{{\sqrt{2}Bsω}}{2R}$ | C. | $\frac{Bsω}{4R}$ | D. | $\frac{Bsω}{2R}$ |
14.甲、乙为两颗地球卫星,其中甲为地球同步卫星,乙的运行高度低于甲的运行高度,两卫星轨道均可视为圆轨道.以下判断正确的是( )
| A. | 乙的速度大于第一宇宙速度 | B. | 甲的运行周期小于乙的周期 | ||
| C. | 甲的加速度小于乙的加速度 | D. | 甲有可能经过北极的正上方 |
4.下列说法正确的是( )
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 当两分子间距离增大时,分子力一定减小而分子势能一定增加 | |
| C. | 热量不会自动地从低温物体传给高温物体而不引起其他变化 | |
| D. | 夏天将密闭有空气的矿泉水瓶放进低温的冰箱中会变扁,此过程中瓶内空气(可看成理想气体)的内能减小,外界对其做功同时向外放热 |
 如图所示,一横截面为圆形的透明玻璃体,真空中一束激光沿平行于直径AB的方向从M点射入玻璃体,其折射光线恰好通过B点,激光在玻璃体中传播的速度为$\frac{{\sqrt{3}c}}{3}$(c为光速),求:
如图所示,一横截面为圆形的透明玻璃体,真空中一束激光沿平行于直径AB的方向从M点射入玻璃体,其折射光线恰好通过B点,激光在玻璃体中传播的速度为$\frac{{\sqrt{3}c}}{3}$(c为光速),求: 利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差,应该选择的实验电路是如图中的甲(选填“甲”或“乙”).
利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差,应该选择的实验电路是如图中的甲(选填“甲”或“乙”).
