题目内容
4.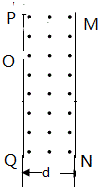 如图所示,竖直放置的足够长绝缘板PQ右方区域垂直纸面向外的匀强磁场,B=5.0×10-2 T,MN是与PQ平行的磁场的右边界,d=0.2,在PQ上的小孔O处有放射源,放射源沿纸面向磁场中各个方向均匀地射出速率为 v=2×106m/s某种带正电的粒子,粒子的质量m=1.6×10-27kg,所带电量q=3.2×10-19C,不计粒子的重力及粒子间的相互作用.
如图所示,竖直放置的足够长绝缘板PQ右方区域垂直纸面向外的匀强磁场,B=5.0×10-2 T,MN是与PQ平行的磁场的右边界,d=0.2,在PQ上的小孔O处有放射源,放射源沿纸面向磁场中各个方向均匀地射出速率为 v=2×106m/s某种带正电的粒子,粒子的质量m=1.6×10-27kg,所带电量q=3.2×10-19C,不计粒子的重力及粒子间的相互作用.(1)求带电粒子在磁场中运动轨迹的半径.
(2)从边界MN射出的粒子在磁场中运动的最短时间为多少?
分析 (1)带电粒子在磁场中做匀速圆周运动,由洛伦兹力充当向心力,由牛顿第二定律求解轨迹半径.
(2)因为粒子运动的轨道半径相同,故弦最短时对应的圆心角最小,运动时间最短,根据几何关系得到最短的弦的大小,再求解最短时间.
解答 解:(1)由洛伦兹力提供向心力得:qvB=m$\frac{{v}^{2}}{r}$
得:r=$\frac{mv}{qB}=\frac{1.6×1{0}^{-27}×2×1{0}^{6}}{3.2×1{0}^{-19}×5.0×1{0}^{-2}}$m=0.2m
(2)因为粒子运动的轨道半径相同,故弦最短时对应的圆心角最小,运动时间最短,显然最短的弦的大小为d,易得此时的圆心角θ=$\frac{π}{3}$
粒子做圆周运动的周期为:T=$\frac{2πr}{v}=\frac{2πm}{qB}$
最短时间为:t=$\frac{θ}{2π}•T=\frac{1}{6}T=\frac{πm}{3qB}$=$\frac{3.14×1.6×1{0}^{-27}}{3×3.2×1{0}^{-19}×5.0×1{0}^{-2}}=1.04×1{0}^{-7}$
答:(1)带电粒子在磁场中的轨迹半径为0.2m;
(2)粒子的周期和从边界MN射出的粒子在磁场中运动的最短时间是1.04×10-7s;
点评 本题中带电粒子在匀强磁场中运动的类型,画出粒子的运动轨迹,运用几何知识和牛顿第二定律研究磁场中轨迹问题.

练习册系列答案
相关题目
14.下列描述的运动,能找到实例的是( )
| A. | 物体运动的速度不断变化,而加速度却等于零 | |
| B. | 物体运动的加速度等于零,而速度却不等于零 | |
| C. | 物体运动的加速度不等于零,而速度保持不变 | |
| D. | 物体作曲线运动,但具有恒定的加速度 |
16.用导热性能良好的材料制成的气体的实验装置,开始时封闭一定长度的空气柱,现向下缓慢压活塞,关闭气体,下列说法正确的是( )
| A. | 外界对气体做功,内能增加 | B. | 体积减小,温度降低 | ||
| C. | 压强变大,温度不变 | D. | 分子平均动能变大 |
14. 如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位移-时间(x-t)图象,由图可知( )
如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位移-时间(x-t)图象,由图可知( )
 如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位移-时间(x-t)图象,由图可知( )
如图所示,直线a和曲线b分别是在平直公路上行驶的汽车a和b的位移-时间(x-t)图象,由图可知( )| A. | 在时刻t1,a车与b车的速率相等 | |
| B. | 在时刻t2,a和b两车的运动方向相同 | |
| C. | 在t1到t2这段时间内,a和b两车的路程相等 | |
| D. | 在t1到t2这段时间内,b车的速率先减小后增大 |
15.如图示,闭合开关S,当滑动变阻器的滑片P向左移动时( )


| A. | 电流表读数变大,电压表读数变小 | B. | 小电珠L变暗 | ||
| C. | 电容器C两极板间的场强变小 | D. | 电源的总功率变小 |
 为测定一只标有12V、24W字样的汽车前灯的伏安特性,实验室能提供以下器材:
为测定一只标有12V、24W字样的汽车前灯的伏安特性,实验室能提供以下器材: 重力为100N的物体A,如图所示悬挂,悬挂OC水平,悬线OB与竖直方向成α=60°角,
重力为100N的物体A,如图所示悬挂,悬挂OC水平,悬线OB与竖直方向成α=60°角,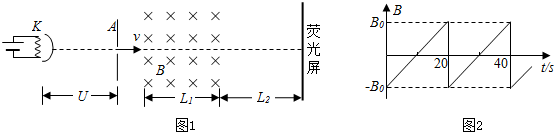
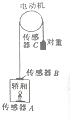 人们平常上下楼乘坐的电梯主要有轿厢、曳引机和对重组成,电动机的主轴带动转轮转动,电动机可以顺时针方向转动,也可逆时针方向转动,这样,在电动机带动下,轿厢可以上升,也可以下降,如图所示,在电梯的轿厢地板上,牵引钢丝与轿厢和对重连接处分别装有力传感器A、B、C,某时刻电梯由低层从静止开始上升时,轿厢内只有一个乘客,乘客脚下的传感器A的示数为660N,牵引钢丝与轿厢连接处传感器B的示数为13200N,牵引钢丝与对重连接处传感器C的示数为9000N,已知乘客质量为60kg,重力加速度g=10m/s2,求
人们平常上下楼乘坐的电梯主要有轿厢、曳引机和对重组成,电动机的主轴带动转轮转动,电动机可以顺时针方向转动,也可逆时针方向转动,这样,在电动机带动下,轿厢可以上升,也可以下降,如图所示,在电梯的轿厢地板上,牵引钢丝与轿厢和对重连接处分别装有力传感器A、B、C,某时刻电梯由低层从静止开始上升时,轿厢内只有一个乘客,乘客脚下的传感器A的示数为660N,牵引钢丝与轿厢连接处传感器B的示数为13200N,牵引钢丝与对重连接处传感器C的示数为9000N,已知乘客质量为60kg,重力加速度g=10m/s2,求