题目内容
19.如图所示的是电视机显像管的原理图.涂有特殊材料的阴极K,在灯丝加热时会逸出电子(初速度可看作零,质量为m,电荷量为-e),逸出的电子经过加速电压为U的电场加速和汇聚后,形成一束很细的电子束射入匀强磁场区.已知磁场的宽度为L1,磁场方向垂直纸面向里,磁感应强度B随时间t变化的关系如图2所示,磁场右侧边界离荧光屏的距离为L2.求: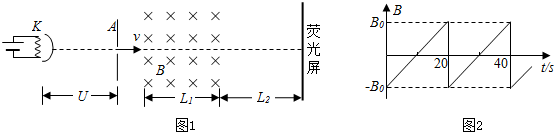
(1)电子进入磁场区时的速度大小;
(2)电子在磁场中的最小偏半径和最大偏转角;
(3)荧光屏发光范围的宽度.(结果以最大半径和最大偏转角表示)
分析 (1)电子在加速电场中,由电场力做正功,获得动能,根据动能定理可求得电子进入磁场区时的速度大小.
(2)电子进入磁场后由洛伦兹力提供向心力,由牛顿第二定律得到轨迹半径表达式,分析半径与B的关系,即可得到最小偏转半径.并由几何知识求出最大偏转角.
(3)由几何知识求解荧光屏发光范围的宽度.
解答 解:(1)电子在加速电场中做加速运动,
由动能定理得:eU=$\frac{1}{2}m{v}_{0}^{2}$-0,解得:v0=$\sqrt{\frac{2eU}{m}}$
(2)电子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,
由牛顿第二定律得:ev0B=m$\frac{{v}_{0}^{2}}{r}$,解得:r=$\frac{m{v}_{0}}{qB}$=$\frac{1}{B}$$\sqrt{\frac{2mU}{e}}$;
由上式可知:B越大,偏转半径r越小,所以由题意可得当B=B0时,粒子半径最小,故最小的偏转半径为
rmin=$\frac{m{v}_{0}}{e{B}_{0}}$=$\frac{1}{{B}_{0}}$$\sqrt{\frac{2mU}{e}}$
而当偏转半径最小时,偏转角度最大,设最大偏转角为α
则 sinα=$\frac{{L}_{1}}{{r}_{min}}$=${L}_{1}{B}_{0}\sqrt{\frac{e}{2mU}}$
得 α=arcsin${L}_{1}{B}_{0}\sqrt{\frac{e}{2mU}}$
(3)荧光屏上发光的范围宽度 d=2$\sqrt{{r}_{min}^{2}-{L}_{1}^{2}}$+L2tanα
答:
(1)电子进入磁场区时的速度大小是$\sqrt{\frac{2eU}{m}}$;
(2)电子在磁场中的最小偏转半径为$\frac{1}{{B}_{0}}$$\sqrt{\frac{2mU}{e}}$,最大偏转角为arcsin${L}_{1}{B}_{0}\sqrt{\frac{e}{2mU}}$;
(3)荧光屏发光范围的宽度为2$\sqrt{{r}_{min}^{2}-{L}_{1}^{2}}$+L2tanα.
点评 本题考查了电子在电场与磁场中的运动,分析清楚电子的运动过程、应用动能定理、牛顿第二定律即可正确解题,解题时注意几何知识的应用.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | ${\;}_{7}^{13}$N和${\;}_{6}^{13}$C互为镜像核 | |
| B. | ${\;}_{7}^{15}$N和${\;}_{8}^{16}$O互为镜像核 | |
| C. | 核反应${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是α衰变 | |
| D. | 将氚核(${\;}_{1}^{3}$H)分解成一个质子和两个中子时一定放出能量 |
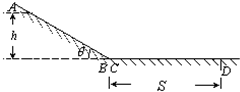 图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计,一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓慢地由D点推回到A点时停下,设滑块与轨道间的摩擦系数为μ,则推力做的功等于( )
图中ABCD是一条长轨道,其中AB段是倾角为θ的斜面,CD是水平的,BC是与AB和CD都相切的一小段圆弧,其长度可以略去不计,一质量为m的小滑块在A点从静止状态释放,沿轨道滑下,最后停在D点,A点和D点的位置如图所示,现用一沿轨道方向的力推滑块,使它缓慢地由D点推回到A点时停下,设滑块与轨道间的摩擦系数为μ,则推力做的功等于( )| A. | μmg(s+$\frac{h}{sinθ}$) | B. | μmg(s+hcotθ) | C. | mgh | D. | 2mgh |
| A. | 只有在静止和匀速直线运动状态,物体才处于平衡状态 | |
| B. | 做竖直上抛运动的物体,上升到最高点时速度为零,此瞬间物体处于平衡状态 | |
| C. | 若一个物体相对另一个物体静止,则此物体处于平衡状态 | |
| D. | 若一个物体所受合外力为零,则此物体处于静止状态 |
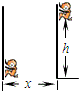 如图所示,在杂技表演中,猴子沿竖直杆向上做初速度为零的匀加速运动,同时人顶着直杆水平匀速移动,若猴子经过3s时间沿杆向上滑动3.6m的高度,同时人顶杆沿水平地面移动的距离为5.4m.已知sin37°=0.6,cos37°=0.8.
如图所示,在杂技表演中,猴子沿竖直杆向上做初速度为零的匀加速运动,同时人顶着直杆水平匀速移动,若猴子经过3s时间沿杆向上滑动3.6m的高度,同时人顶杆沿水平地面移动的距离为5.4m.已知sin37°=0.6,cos37°=0.8.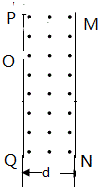 如图所示,竖直放置的足够长绝缘板PQ右方区域垂直纸面向外的匀强磁场,B=5.0×10-2 T,MN是与PQ平行的磁场的右边界,d=0.2,在PQ上的小孔O处有放射源,放射源沿纸面向磁场中各个方向均匀地射出速率为 v=2×106m/s某种带正电的粒子,粒子的质量m=1.6×10-27kg,所带电量q=3.2×10-19C,不计粒子的重力及粒子间的相互作用.
如图所示,竖直放置的足够长绝缘板PQ右方区域垂直纸面向外的匀强磁场,B=5.0×10-2 T,MN是与PQ平行的磁场的右边界,d=0.2,在PQ上的小孔O处有放射源,放射源沿纸面向磁场中各个方向均匀地射出速率为 v=2×106m/s某种带正电的粒子,粒子的质量m=1.6×10-27kg,所带电量q=3.2×10-19C,不计粒子的重力及粒子间的相互作用.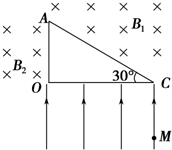 有一直角三角形OAC,OC水平且长为12 cm,其下方存在垂直OC向上的匀强电场,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度为B1=1 T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从M点由静止释放,MC=8 cm,MC⊥OC,粒子经电场加速后进入磁场,恰好经A点到达O点,不计粒子重力,求:
有一直角三角形OAC,OC水平且长为12 cm,其下方存在垂直OC向上的匀强电场,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度为B1=1 T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从M点由静止释放,MC=8 cm,MC⊥OC,粒子经电场加速后进入磁场,恰好经A点到达O点,不计粒子重力,求: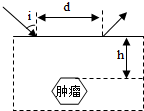 “B超”可用于探测人体内脏的病变状况,如图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为$\frac{sin{θ}_{1}}{sin{θ}_{2}}$=$\frac{{v}_{1}}{{v}_{2}}$(式中θ1是入射角,θ2是折射角,v1、v2分别是超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同.已知v2=0.9v1,入射点与出射点之间的距离是d,入射角是i,肿瘤的反射面恰好与肝脏表面平行,求解肿瘤离肝脏表面的深度h为多少?
“B超”可用于探测人体内脏的病变状况,如图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为$\frac{sin{θ}_{1}}{sin{θ}_{2}}$=$\frac{{v}_{1}}{{v}_{2}}$(式中θ1是入射角,θ2是折射角,v1、v2分别是超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同.已知v2=0.9v1,入射点与出射点之间的距离是d,入射角是i,肿瘤的反射面恰好与肝脏表面平行,求解肿瘤离肝脏表面的深度h为多少?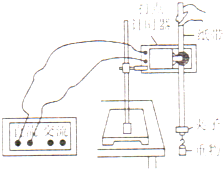 在一次实验探究课上,某同学利用自由落体来探究机械能守恒定律,该同学开始实验时 的情形如图所示,他将电磁打点计时器接通低压电源后释放纸带.
在一次实验探究课上,某同学利用自由落体来探究机械能守恒定律,该同学开始实验时 的情形如图所示,他将电磁打点计时器接通低压电源后释放纸带.