题目内容
17. 如图所示,在倾角为θ=37°的粗糙斜面底端,有一小滑块甲(可视为质点)以v0=24.8m/s的初速度沿斜面上滑,与此同时,另一小球乙(也可视为质点)从斜面顶端以一定的初速度v水平抛出,两者在3s末相遇.已知小滑块甲与斜面间的动摩擦因数为μ=0.8,取重力加速度为g=10m/s2,sin 37°=0.6,cos 37°=0.8.不计滑块与小球运动时所受的空气阻力.试分析:
如图所示,在倾角为θ=37°的粗糙斜面底端,有一小滑块甲(可视为质点)以v0=24.8m/s的初速度沿斜面上滑,与此同时,另一小球乙(也可视为质点)从斜面顶端以一定的初速度v水平抛出,两者在3s末相遇.已知小滑块甲与斜面间的动摩擦因数为μ=0.8,取重力加速度为g=10m/s2,sin 37°=0.6,cos 37°=0.8.不计滑块与小球运动时所受的空气阻力.试分析:(1)小球乙的初速度v的大小是多少?
(2)斜面的总长度L的大小是多少?
分析 (1)小球做平抛运动,根据平抛运动的特点求得初速度;
(2)滑块上滑做减速运动,根据牛顿第二定律求得加速度,利用运动学公式求得上滑的位移,结合平抛运动即可求得斜面的长度,
解答 解:(1)小球做平抛运动,3s内竖直下落的高度h=$\frac{1}{2}g{t}^{2}=\frac{1}{2}×10×{3}^{2}m=45m$
水平方向的位移$x=\frac{h}{tan37°}=60m$
水平方向匀速运动,则$v=\frac{x}{t}=\frac{60}{3}m/s=20m/s$
(2)滑块沿斜面下滑的距离$L=\sqrt{{x}^{2}+{h}^{2}}=75m$
对滑块甲受力分析,根据牛顿第二定律可知mgsinθ+μmgcosθ=ma
解得a=12.4m/s2
滑块上滑减速到零所需时间${t}_{0}=\frac{{v}_{0}}{a}=2s$
2s后由于mgsinθ<μmgcosθ,故滑块静止在斜面上
3s内的位移为$L′=\frac{{v}_{0}}{2}{t}_{0}=24.8m$
斜面的长度L总=L+L′=99.8m
答:(1)小球乙的初速度v的大小是20m/s
(2)斜面的总长度L的大小是99.8m
点评 本题主要考查了平抛运动和匀减速直线运动,关键是抓住滑块减速到零后不再下滑而是静止在斜面上即可求得

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
20.一质点在做匀加速直线运动,加速度为a,在时间t内速度变为原来的3倍,则该质点在时间t内的位移为( )
| A. | $\frac{1}{2}$at2 | B. | at2 | C. | $\frac{3}{2}$at2 | D. | 2at2 |
9.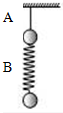 如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
 如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )| A. | aA=0,aB=g | B. | aA=g,aB=0 | C. | aA=0,aB=2g | D. | aA=2g,aB=0 |
7.质量为m的物体,从地面以$\frac{g}{5}$的加速度加速上升h高处.下列说法中正确的是( )
| A. | 物体的重力势增加$\frac{1}{5}$mgh | B. | 物体的动能增加$\frac{1}{5}$mgh | ||
| C. | 物体的机械能增加$\frac{1}{5}$mgh | D. | 物体的机械能增加$\frac{4}{5}$mgh |
 一辆汽车质量m=1×103kg,在水平路面上由静止开始做直线运动,所受阻力恒定不变,牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示,则汽车在BC段的运动为加速度减小的加速运动.若发动机的最大牵引力为3×103N,最大输出功率Pm=2×104W,图中的v2为汽车的最大速度,则汽车在图示的ABC运动过程中,当速度v=10m/s时,发动机的瞬时输出功率P=2×104W.
一辆汽车质量m=1×103kg,在水平路面上由静止开始做直线运动,所受阻力恒定不变,牵引力F与车速的倒数$\frac{1}{v}$的关系如图所示,则汽车在BC段的运动为加速度减小的加速运动.若发动机的最大牵引力为3×103N,最大输出功率Pm=2×104W,图中的v2为汽车的最大速度,则汽车在图示的ABC运动过程中,当速度v=10m/s时,发动机的瞬时输出功率P=2×104W. 如图所示,一个质量为5kg的光滑球放在质量为20kg的小车中,小车顶板AB与底板CD间的距离恰好与小球直径相等,侧壁AD与顶板的夹角为45°,整个装置放在光滑水平面上,现对小车施加F=500N的水平拉力.求
如图所示,一个质量为5kg的光滑球放在质量为20kg的小车中,小车顶板AB与底板CD间的距离恰好与小球直径相等,侧壁AD与顶板的夹角为45°,整个装置放在光滑水平面上,现对小车施加F=500N的水平拉力.求
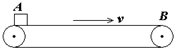 水平传送带以v=1.5m/s速度匀速运动,传送带AB两端距离为6.75m,将物体轻放在传送带的A端,它运动到传送带另一端B所需时间为6s,求:
水平传送带以v=1.5m/s速度匀速运动,传送带AB两端距离为6.75m,将物体轻放在传送带的A端,它运动到传送带另一端B所需时间为6s,求: