题目内容
11.下列说法正确的是( )| A. | 一对平衡力所做功之和一定为零,一对作用力与反作用力所做功之和也一定为零 | |
| B. | 一对平衡力的冲量之和一定为零,一对作用力与反作用力的冲量之和也一定为零 | |
| C. | 物体所受合力冲量的方向一定与物体动量的变化方向相同,不一定与物体的末动量方向相同 | |
| D. | 火箭喷出的燃气的速度越大、火箭的质量比越大,则火箭获得的速度就越大 |
分析 功是力与力的作用点在力的方向上的位移的乘积;冲量是力与时间的乘积,根据动量定理,合力的冲量等于物体动量的该变量;火箭的质量比是火箭起飞时的质量(包括推进剂在内的质量)与发动机关机(熄火)时刻的火箭质量(火箭的结构质量,即净重)之比,因此,质量比大,就意味着火箭的结构质量小,所携带的推进剂多.
解答 解:A、合力的功等于各个分力的功的代数和,一对平衡力的合力为零,故一对平衡力所做功之和一定为零;
一对作用力与反作用力作用在两个不同的物体上,两个力的作用点的位移不一定相等,故一对作用力与反作用力所做功之和可以为零;故A错误;
B、冲量是力与时间的乘积,故一对平衡力的冲量大小相等、方向相反,故一对平衡力的冲量之和一定为零;
一对作用力与反作用力大小相等、方向相反、作用时间相等,故一对作用力与反作用力的冲量之和也一定为零;故B正确;
C、根据动量定理,物体所受合力冲量的方向一定与物体动量的变化方向相同,不一定与物体的末动量方向相同,故C正确;
D、火箭是利用反冲的原理工作的,根据动量守恒定律,有:0=(M-m)v-mv′;
解得:v′=$\frac{M-m}{m}v$;
喷出的燃气的速度越大、火箭的质量比越大,则火箭能够获得的速度就越大,故D正确;
故选:BCD
点评 本题考查了功、动量、冲量、动量定理,关键是记住平衡力的冲量、功,相互作用力的功、冲量的关系,基础题目.

练习册系列答案
相关题目
1.关于地球同步卫星,下列说法正确的是( )
| A. | 它可以定位在夷陵中学的正上空 | |
| B. | 地球同步卫星的角速度虽被确定,但高度和线速度可以选择,高度增加,线速度减小,高度降低,线速度增大 | |
| C. | 它运行的线速度一定小于第一宇宙速度 | |
| D. | 它运行的线速度一定介于第一宇宙速度和第二宇宙速度之间 |
2.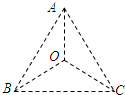 如图所示,在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q,此时三角形中心O处场强大小为E,电势为U,选无穷远处电势为零,现将A处的-Q换成+Q,其他条件不变,则中心O处场强大小和电势分别为( )
如图所示,在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q,此时三角形中心O处场强大小为E,电势为U,选无穷远处电势为零,现将A处的-Q换成+Q,其他条件不变,则中心O处场强大小和电势分别为( )
 如图所示,在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q,此时三角形中心O处场强大小为E,电势为U,选无穷远处电势为零,现将A处的-Q换成+Q,其他条件不变,则中心O处场强大小和电势分别为( )
如图所示,在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q,此时三角形中心O处场强大小为E,电势为U,选无穷远处电势为零,现将A处的-Q换成+Q,其他条件不变,则中心O处场强大小和电势分别为( )| A. | E,3U | B. | 0,3U | C. | E,U | D. | 0,U |
19. 两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点O)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点O)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
 两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点O)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )
两个点电荷Q1、Q2固定于x轴上,将一带正电的试探电荷从足够远处沿x轴负方向移近Q2(位于坐标原点O)的过程中,试探电荷的电势能Ep随位置变化的关系如图所示,则下列判断正确的是( )| A. | M点电势为零,N点场强不为零 | |
| B. | M点场强为零,N点电势为零 | |
| C. | Q1带负电,Q2带正电,且Q2电荷量较小 | |
| D. | Q1带正电,Q2带负电,且Q2电荷量较小 |
6. 如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )
如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )
 如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )
如图是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )| A. | 该金属的逸出功等于E | |
| B. | 该金属的逸出功等于hνc | |
| C. | 入射光的频率为2νc时,产生的光电子的最大初动能为E | |
| D. | 入射光的频率为2νc时,产生的光电子的最大初动能为2E |
16.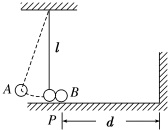 如图所示,有一个摆长为l的单摆,现将摆球A拉离平衡位置一个很小的角度,然后由静止释放,A摆至平衡位置P时,恰与静止在P处的B球发生碰撞,碰后A继续向右摆动,B球以速度v沿光滑水平面向右运动,与右侧的墙壁碰撞后以原速率返回,当B球重新回到位置P时能与A再次相遇,则位置P与墙壁间的距离d可能为( )
如图所示,有一个摆长为l的单摆,现将摆球A拉离平衡位置一个很小的角度,然后由静止释放,A摆至平衡位置P时,恰与静止在P处的B球发生碰撞,碰后A继续向右摆动,B球以速度v沿光滑水平面向右运动,与右侧的墙壁碰撞后以原速率返回,当B球重新回到位置P时能与A再次相遇,则位置P与墙壁间的距离d可能为( )
 如图所示,有一个摆长为l的单摆,现将摆球A拉离平衡位置一个很小的角度,然后由静止释放,A摆至平衡位置P时,恰与静止在P处的B球发生碰撞,碰后A继续向右摆动,B球以速度v沿光滑水平面向右运动,与右侧的墙壁碰撞后以原速率返回,当B球重新回到位置P时能与A再次相遇,则位置P与墙壁间的距离d可能为( )
如图所示,有一个摆长为l的单摆,现将摆球A拉离平衡位置一个很小的角度,然后由静止释放,A摆至平衡位置P时,恰与静止在P处的B球发生碰撞,碰后A继续向右摆动,B球以速度v沿光滑水平面向右运动,与右侧的墙壁碰撞后以原速率返回,当B球重新回到位置P时能与A再次相遇,则位置P与墙壁间的距离d可能为( )| A. | $\frac{πv}{4}\sqrt{\frac{l}{g}}$ | B. | $\frac{πv}{2}\sqrt{\frac{l}{g}}$ | C. | $\frac{3πv}{4}\sqrt{\frac{l}{g}}$ | D. | πv$\sqrt{\frac{l}{g}}$ |
3.(多选)下列说法中正确的是( )
| A. | 某点瞬时速度的方向就在曲线上该点的切线上 | |
| B. | 变速运动一定是曲线运动 | |
| C. | 曲线运动一定是变速运动 | |
| D. | 曲线运动不一定是变速运动 |
13.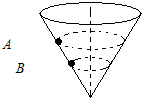 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 线速度vA>vB | B. | 角速度ωA=ωB | C. | 向心力FA=FB | D. | 向心加速度aA<aB |
 如图所示,电源的电压保持不变,小灯泡L标有“6V 3W”字样,滑动变阻器R1的阻值变化范围为0~20Ω,电阻R2的阻值为12Ω.灯丝的电阻随温度的变化忽略不计.
如图所示,电源的电压保持不变,小灯泡L标有“6V 3W”字样,滑动变阻器R1的阻值变化范围为0~20Ω,电阻R2的阻值为12Ω.灯丝的电阻随温度的变化忽略不计.