题目内容

2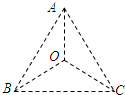．如图所示，在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q，此时三角形中心O处场强大小为E，电势为U，选无穷远处电势为零，现将A处的-Q换成+Q，其他条件不变，则中心O处场强大小和电势分别为（　　）
A．E，3UB．0，3UC．E，UD．0，U

分析 根据对称性和电场的叠加原理分析场强的大小．根据三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q时，-Q与+Q在O点的电势为零，从而确定出另一个+Q在O点的电势，从而能求出将A处的-Q换成+Q后O点的电势．

解答 解：将A处的-Q换成+Q，三个+Q在O点产生的场强大小相等，夹角均为120°，根据电场的叠加原理可知，O处的场强大小为0．
根据三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q时，-Q与+Q连线的垂直平分线是一条等势线，其电势与无穷远处电势相等，则-Q与+Q形成的电场在O点的电势为零，根据电场的叠加原理知，另一个+Q在O点的电势为U，所以将A处的-Q换成+Q后O点的电势为 3U．故B正确．
故选：B

点评 本题是电场的叠加问题，关键要掌握等量异种电荷等势面的分布情况，知道它们的连线的垂直平分线是一个等势面，且一直延伸到无穷远．

练习册系列答案
相关题目
12．关于功率，下列正确的是（　　）
A．只知道W和t就可由P=$\frac{W}{t}$计算t时刻的功率
B．由P=FV可知汽车发动机的功率一定与F和v的乘积成正比
C．当汽车发动机功率一定时，牵引力与速度成反比
D．要提高汽车行驶的最大速度，一定要提高发动机的额定功率
13．某金属的逸出功为2.6eV，这意味着（　　）
A．这种金属内部的电子克服原子核引力做2.6 eV的功即可脱离该金属表面
B．这种金属内部的电子只要获得2.6eV的能量即可脱离该金属表面
C．要使这种金属有电子逸出，入射光子的能量必须大于2.6 eV
D．这种金属受到光照时若有电子逸出，则电子离开金属表面时的动能至少等于2.6 eV
10．物体受到合力F的作用，由静止开始运动，力F随时间变化的图象如图所示，下列说法中正确的是（　　）
A．该物体将始终向一个方向运动
B．3s末该物体回到原出发点
C．1～2s内，力F的冲量等于零，功也等于零
D．2～4s内，力F的冲量不等于零，功却等于零
17．一物体做匀速圆周运动，关于向心加速度和向心力说法正确的是（　　）
A．向心加速度大小不变，所以匀速圆周运动是匀变速曲线运动
B．向心加速度方向可以与向心力不同
C．向心力是物体维持匀速圆周运动的条件，施力物是物体本身
D．向心力产生向心加速度，使物体运动方向不断变化变化
7．小明坐在由上海开往北京的高速列车上感觉自己静止不动，他所选择的参考系可能是（　　）
A．铁轨B．车厢
C．铁路旁的树木D．车厢内走动的乘客
14．某同学用电阻箱、电压表测量不通电源的电动势和内阻，因所测电源的内阻r较小，因此她在电路中接入了一个阻值为2.00Ω的定值电阻R0，所用电路如图甲所示．
（1）请按图甲用笔画代替导线将如图乙所示的器材连接成完整的实验电路．

（2）闭合开关S，调整电阻箱的阻值R，读出电压表相应的示数U、R数据，为了比较准确地得出结论，小王同学准备用图象来处理实验数据，图象的纵坐标表示电压表读数U的倒数$\frac{1}{U}$，则图象的横坐标表示的物理量应该是$\frac{1}{R}$才能使做出的图线为一条直线．
11．下列说法正确的是（　　）
A．一对平衡力所做功之和一定为零，一对作用力与反作用力所做功之和也一定为零
B．一对平衡力的冲量之和一定为零，一对作用力与反作用力的冲量之和也一定为零
C．物体所受合力冲量的方向一定与物体动量的变化方向相同，不一定与物体的末动量方向相同
D．火箭喷出的燃气的速度越大、火箭的质量比越大，则火箭获得的速度就越大
4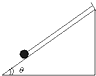．一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端，如图，斜面静止时，球紧靠在斜面上，绳与斜面平行，不计摩擦，当斜面以10m/s2的加速度向右做加速运动时，则（　　）（sin53°=0.8，cos53°=0.6，g=10m/s2 ）
A．绳的拉力为1.60NB．绳的拉力为2$\sqrt{2}$N
C．斜面对小球的弹力为1.20ND．斜面对小球的弹力为0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网