题目内容
20．
如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω转动，盘面上离转轴距离r处有一小物体与圆盘始终保持相对静止．物体与盘面间的动摩擦因数为μ（设最大静摩擦力等于滑动摩擦力），盘面与水平面的夹角为θ，重力加速度为g，则ω的最大值是（ ）| A． | $\sqrt{\frac{g（μcosθ-sinθ）}{r}}$ | B． | $\sqrt{\frac{g（μsinθ-cosθ）}{r}}$ | C． | $\sqrt{\frac{g（cosθ-μsinθ）}{r}}$ | D． | $\sqrt{\frac{g（sinθ-μcosθ）}{r}}$ |
分析 当物体转到圆盘的最低点，由重力沿斜面向下的分力和最大静摩擦力的合力提供向心力时，角速度最大，由牛顿第二定律求出最大角速度．
解答 解：当物体转到圆盘的最低点，所受的静摩擦力沿斜面向上达到最大时，角速度最大，由牛顿第二定律得：
μmgcosθ-mgsinθ=mω2r
则ω=$\sqrt{\frac{g（μcosθ-sinθ）}{r}}$，故A正确．
故选：A
点评 本题关键要分析向心力的来源，明确角速度在什么位置最大，由牛顿第二定律进行解题．
练习册系列答案
相关题目
9．
如图所示，粗细均匀的电阻丝制成的长方形导线框abcd处在匀强磁场中，磁场方向垂直于线框平面，另一种材料的导体棒MN与导线框保持良好接触并在外力作用下从导线框左端匀速滑到右端，在此过程中，导线框上消耗的电功率P的变化情况可能为（ ）
如图所示，粗细均匀的电阻丝制成的长方形导线框abcd处在匀强磁场中，磁场方向垂直于线框平面，另一种材料的导体棒MN与导线框保持良好接触并在外力作用下从导线框左端匀速滑到右端，在此过程中，导线框上消耗的电功率P的变化情况可能为（ ）| A． | 逐渐增大 | B． | 先增大后减小 | ||
| C． | 先减小后增大 | D． | 增大、减小、再增大、再减小 |
10．
小球由空中某点开始下落，与地面相碰后，反弹至某一高度，小球下落和弹起的过程中沿同一直线运动，不计小球与地面碰撞的时间，小球的速度图象如图所示，设小球运动过程中受到的阻力大小恒定，取g=10m/s2，则（ ）
小球由空中某点开始下落，与地面相碰后，反弹至某一高度，小球下落和弹起的过程中沿同一直线运动，不计小球与地面碰撞的时间，小球的速度图象如图所示，设小球运动过程中受到的阻力大小恒定，取g=10m/s2，则（ ）| A． | 小球下落的加速度是10m/s2 | B． | 小球向上弹起时的速度是6m/s | ||
| C． | 小球在此过程中通过的路程为5.5m | D． | 小球受到的阻力是重力的0.2倍 |
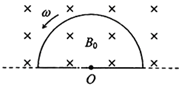如图，均匀磁场中有一由半圆弧半径为L及其直径构成的导线框，半圆直径与磁场边缘重合； 磁场方向垂直于半圆面（纸面）向里，磁感应强度大小为B0．使该线框由图示位置从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周，在线框中产生感应电流．
15．
“套圈圈”是小孩和大人都喜爱的一种游戏．某小孩和大人直立在界外，在同一竖直线上不同高度分别水平抛出小圆环，并恰好套中前方同一物体．假设小圆环的运动可视为平抛运动，则（ ）
“套圈圈”是小孩和大人都喜爱的一种游戏．某小孩和大人直立在界外，在同一竖直线上不同高度分别水平抛出小圆环，并恰好套中前方同一物体．假设小圆环的运动可视为平抛运动，则（ ）| A． | 大人抛出的圆环运动时间较短 | |
| B． | 大人应以较小的速度抛出圆环 | |
| C． | 小孩应以较小的速度抛出圆环 | |
| D． | 小孩抛出的圆环单位时间内速度变化量较小 |
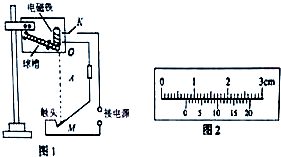如图1，竖直平面内固定一斜槽，斜槽中放有若干个直径均为d的相同小铁球，紧靠斜槽末端固定有电磁铁，闭合开关K，电磁铁吸住第一个小球，第二个小球处于斜槽末端被第一个小球阻挡而不落下．轻敲金属片M，M与触点分离，第一个小球从O点开始下落，M迅速恢复接触，电磁铁又吸住第二个小球，当第一个小球撞击M时，第二个小球又开始下落…
如图所示是某次平抛实验中用描点法在坐标纸上记录的三个点A，B，C．已知每个小方格的边长相同，请完成以下问题：