题目内容
10. 如图所示,两块相同平板P1、P2置于光滑水平面上,质量均为m.P2的右端固定一轻质弹簧,弹簧的自由端恰好在P2的左端A点.物体P置于P1的最右端,质量为2m且可以看作质点.P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短,碰撞后P1与P2粘连在一起,P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内).P与P2之间的动摩擦因数为μ,求
如图所示,两块相同平板P1、P2置于光滑水平面上,质量均为m.P2的右端固定一轻质弹簧,弹簧的自由端恰好在P2的左端A点.物体P置于P1的最右端,质量为2m且可以看作质点.P1与P以共同速度v0向右运动,与静止的P2发生碰撞,碰撞时间极短,碰撞后P1与P2粘连在一起,P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内).P与P2之间的动摩擦因数为μ,求(1)P1、P2刚碰完时的共同速度v1和P的最终速度v2;
(2)此过程中弹簧最大压缩量x.
分析 (1)P1、P2碰撞过程,由动量守恒定律列出等式.对P1、P2、P系统,由动量守恒定律求解.
(2)根据能量守恒定律求出弹簧的最大压缩量大小.
解答 解:(1)规定向右为正方向,碰撞时由动量守恒定律可得:(m+2m)v0=2mv0+(m+m)v1
解得:${v_1}=\frac{1}{2}{v_0}$
规定向右为正方向,由于物体P与P1、P2之间的力为内力,三者整体由动量守恒定律可得:(m+2m)v0=(m+m+2m)v2
解得:${v_2}=\frac{3}{4}{v_0}$
(2)整个过程能量守恒定律可得:$\frac{1}{2}(m+m)v_1^2+\frac{1}{2}2mv_0^2=\frac{1}{2}(m+m+2m)v_2^2+μ•2mg•2x$
解得:$x=\frac{v_0^2}{32μg}$.
答:(1)P1、P2刚碰完时的共同速度为$\frac{1}{2}{v}_{0}$,P的最终速度为$\frac{3{v}_{0}}{4}$;
(2)此过程中弹簧最大压缩量x为$\frac{{{v}_{0}}^{2}}{32μg}$.
点评 本题综合考查了动量守恒定律、能量守恒定律,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
20.如图甲所示,有一绝缘的竖直圆环,圆环上均匀分布着正电荷.一光滑细杆沿垂直圆环平面的轴线穿过圆环,细杆上套有一个质量为m=10g的带正电的小球,小球所带电荷量q=5.0×10-4C,让小球从C点由静止释放,其沿细杆由C经B向A运动的v-t图象如图乙所示.且已知小球运动到B点时,速度图象的切线斜率最大(图中标出了该切线).下列说法正确的是( )
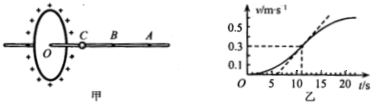

| A. | 在O点右侧杆上,B点场强最大,场强大小为E=1.2V/m | |
| B. | 由C到A的过程中,小球的电势能先减小后变大 | |
| C. | 沿着C到A的方向,电势先降低后升高 | |
| D. | C、B两点间的电势差UCB=0.9V |
5.如图为小型交流发电机的示意图,线圈绕垂直于磁场方向的水平轴OO′沿逆时针方向匀速转动,转速为50r/s,线圈的电阻为r=20Ω,电阻R=100Ω,R0=10Ω,降压变压器原副线圈匝数比为10:1,电压表的示数为10V,如果从图示位置开始计时,下列说法中正确的是( )
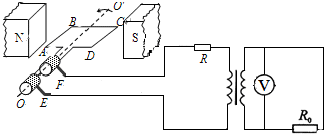

| A. | 变压器原线圈两端的电压为100 V | |
| B. | 电阻R的功率为10W | |
| C. | 电动势的有效值为110 V | |
| D. | 电动势瞬时值表达式为e=112$\sqrt{2}$cos100πtV |
15. 假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )
假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )
 假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )
假设在宇宙中存在这样的三个天体a、b、c,如图所示,天体a和b以相同角速度绕天体c做匀速圆周运动.以下说法正确的是( )| A. | 天体a做圆周运动的加速度大于天体b做圆周运动的加速度 | |
| B. | 天体a做圆周运动的速度小于天体b做圆周运动的速度 | |
| C. | 天体b做圆周运动的向心力大于天体c对它的万有引力 | |
| D. | 天体b做圆周运动的向心力由天体a和天体c对它的万有引力共同提供 |
2. 将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F的最小值为( )
将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F的最小值为( )
 将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F的最小值为( )
将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F的最小值为( )| A. | mg | B. | $\frac{\sqrt{3}}{3}$mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | $\frac{1}{2}$mg |
19. 由中国提供永磁体的阿尔法磁谱仪的原理如图所示,其主要使命是探索宇宙中的反物质,所谓反物质,即质量与正粒子相等,带电量与正粒子相等但符号相反.假设使一束质子、反质子、α粒子、α反粒子组成的射线通过OO′进入匀强磁场B2中形成四条径迹,则( )
由中国提供永磁体的阿尔法磁谱仪的原理如图所示,其主要使命是探索宇宙中的反物质,所谓反物质,即质量与正粒子相等,带电量与正粒子相等但符号相反.假设使一束质子、反质子、α粒子、α反粒子组成的射线通过OO′进入匀强磁场B2中形成四条径迹,则( )
 由中国提供永磁体的阿尔法磁谱仪的原理如图所示,其主要使命是探索宇宙中的反物质,所谓反物质,即质量与正粒子相等,带电量与正粒子相等但符号相反.假设使一束质子、反质子、α粒子、α反粒子组成的射线通过OO′进入匀强磁场B2中形成四条径迹,则( )
由中国提供永磁体的阿尔法磁谱仪的原理如图所示,其主要使命是探索宇宙中的反物质,所谓反物质,即质量与正粒子相等,带电量与正粒子相等但符号相反.假设使一束质子、反质子、α粒子、α反粒子组成的射线通过OO′进入匀强磁场B2中形成四条径迹,则( )| A. | 1和2是反粒子径迹 | B. | 3和4是反粒子径迹 | ||
| C. | 2为反质子径迹 | D. | 4为α粒子径迹 |

