题目内容
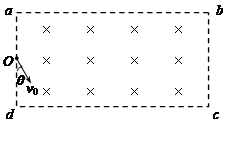
如图所示，一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场，在ad边中点O，方向垂直磁场向里射入速度方向跟ad边夹角θ =30°、大小为v0的带正电粒子，已知粒子质量为m，电量为q，ad边长为L，ab边足够长，粒子重力不计，求：①粒子能从ab边上射出磁场的速度v0的大小范围.②控制带电粒子的速度使其不从cd边射出，求粒子在磁场中运动的最长和最短时间．
①若粒子速度为v0，则qv0B =…（2分）
设圆心在O1处，对应圆弧与ab边相切，
相应速度为v01，则 R1＋R1sinθ =…（3分）
类似地，设圆心在O2处，对应圆弧与cd边相切，
相应速度为v02，则 R2－R2sinθ =………………………………………………（3分）
所以粒子能从ab边上射出磁场的v0应满足＜v0≤
……………………（2分）
②在磁场中运动的半径r≤R1时，运动时间最长，弧所对圆角为（2π－2θ），
由t =及T =
， 最长时间为t1 =
=
………………（4分） 对应圆弧与cd边相切时运动时间最短，最短时间为t 2=
=
………（4分）
解析:略
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
如图所示，一足够长的光滑斜面倾角为30°，斜面AB与水平面BC平滑连接．一物体置于水平面上的D点，D点距B点d=3m，物体与水平面的动摩擦因数为μ=0.2．现给物体一个向左初速度v0=4m/s，求物体经多长时间物体经过B点？（重力加速度g=10m/s2）
如图所示，一足够长的固定斜面与水平方向的夹角为θ=37°，物体B与斜面间的动摩擦因数为μ=0.5．将物体A以初速度v0从斜面顶端水平抛出的同时，物体B在斜面上距顶端L=16.5m处由静止释放，经历时间t，物体A第一次落到斜面上时，恰与物体B相碰，已知sin37°=0.6，cos37°=0.8，g=10m/s2，不计空气阻力，两物体都可视为质点．求：v0和t的大小．
如图所示，一足够长的木板静止在光滑水平面上，一物块静止在木板上，木板和物块间有摩擦．现用水平力向右拉木板，当物块相对木板滑动了一段距离但仍有相对运动时，撤掉拉力，此后木板和物块相对于水平面的运动情况为（ ）
（2011?通州区模拟）如图所示，一足够长的平面框架宽L=0.3m，与水平面成θ=37°角，上下两端各有一个电阻R0=2Ω，框架其它部分的电阻不计，垂直于框架平面的方向上存在向上的匀强磁场，磁感应强度B=1T．金属杆ab长为L=0.3m，质量m=1kg，电阻r=2Ω，与框架的动摩擦因数μ=0.5，以初速度v0=10m/s向上滑行．杆ab上升到最高点的过程中，上端电阻R0产生的热量Q0=5J，g取10m/s2，求：
如图所示，一足够长的光滑斜面，倾角为θ，一弹簧上端固定在斜面的顶端，下端与物体b相连，物体b上表面粗糙，在其上面放一物体a，a、b间的动摩擦因数为μ（μ＞tanθ），将物体a、b从O点由静止开始释放，释放时弹簧恰好处于自由伸长状态，当b滑到A点时，a刚好从b上开始滑动；滑到B点时a刚好从b上滑下，b也恰好速度为零，设a、b间的最大静摩擦力等于滑动摩擦力．下列对物体a、b运动情况描述正确的是（ ）