题目内容
7.设想在深太空探测中,一个探测器到达深太空中的一颗外星球(不考虑自传)开始探测实验.首先测出在外星球近地环绕的周期为T,着陆后竖直上抛一个小球,用速度传感器测出上抛的初速度v,用秒表测出落回抛出点的时间t,则根据上述测量的量不能算出的物理量是( )| A. | 该外星球的密度 | B. | 探测器近地环绕时的线速度 | ||
| C. | 该外星球的半径 | D. | 探测器近地环绕时的向心加速度 |
分析 根据探测器绕地球做匀速圆周运动,万有引力提供向心力,在星球表面重力等于万有引力,结合密度公式,线速度及向心加速度即可求解.
解答 解:A、探测器近地环绕时,看成做匀速圆周运动,由万有引力提供向心力可得$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R=mg$,着陆后由竖直上抛可得$v=g•\frac{t}{2}$及$M=ρ•\frac{4}{3}π{R}_{\;}^{3}$,化简得$ρ=\frac{3π}{G{T}_{\;}^{2}}$,可见要计算外星球的密度,一定要知道万有引力常量,故该外星球的密度不能算出;故A不能算出
BCD、探测器近地环绕时,根据万有引力提供向心力,有G$\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$=mg,得$g=\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$,有竖直上抛运动$v=g•\frac{t}{2}$得$g=\frac{2v}{t}$,联立得$R=\frac{v{T}_{\;}^{2}}{2{π}_{\;}^{2}t}$,所以该外星球的半径可以算出;根据$v=\frac{2πR}{T}$及$a={ω}_{\;}^{2}R=(\frac{2π}{T})_{\;}^{2}R$,探测器近地环绕的线速度、向心加速度均可以算出.故BCD能算出
本题选不能算出的,故选:A
点评 解决本题的关键知道卫星在表面所受的重力等于所受的万有引力,结合万有引力提供向心力进行求解.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
16. 如图所示,轻弹簧上端固定,下端悬挂一质量为m的条形磁铁,磁铁穿过固定的水平闭合金属线圈.将磁铁托起到弹簧压缩x后由静止放开,磁铁会上下运动并逐渐停下来,静止时弹簧伸长x.不计空气阻力,重力加速度为g,弹簧始终在弹性限度内,则( )
如图所示,轻弹簧上端固定,下端悬挂一质量为m的条形磁铁,磁铁穿过固定的水平闭合金属线圈.将磁铁托起到弹簧压缩x后由静止放开,磁铁会上下运动并逐渐停下来,静止时弹簧伸长x.不计空气阻力,重力加速度为g,弹簧始终在弹性限度内,则( )
 如图所示,轻弹簧上端固定,下端悬挂一质量为m的条形磁铁,磁铁穿过固定的水平闭合金属线圈.将磁铁托起到弹簧压缩x后由静止放开,磁铁会上下运动并逐渐停下来,静止时弹簧伸长x.不计空气阻力,重力加速度为g,弹簧始终在弹性限度内,则( )
如图所示,轻弹簧上端固定,下端悬挂一质量为m的条形磁铁,磁铁穿过固定的水平闭合金属线圈.将磁铁托起到弹簧压缩x后由静止放开,磁铁会上下运动并逐渐停下来,静止时弹簧伸长x.不计空气阻力,重力加速度为g,弹簧始终在弹性限度内,则( )| A. | 弹簧处于原长时,磁铁的加速度可能大于g | |
| B. | 磁铁中央通过线圈时,线圈中感应电流最大 | |
| C. | 磁铁向下运动时,线圈受到的安培力方向向上 | |
| D. | 线圈在整个过程中产生的焦耳势为2mgx |
17.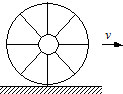 如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
 如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )| A. | 若车轮转速为3.75r/s,则观众觉得车轮是不动的 | |
| B. | 若车轮转速为30r/s,则观众觉得车轮是倒转的 | |
| C. | 若车轮转速为31r/s,则观众觉得车轮是倒转的 | |
| D. | 若车轮转速为29r/s,则观众觉得车轮是倒转的 |
12.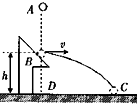 如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
 如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )| A. | A、B两点间的距离为$\frac{h}{2}$ | B. | A、B两点间的距离为h | ||
| C. | C、D两点间的距离为2h | D. | C、D两点间的距离为$\frac{2\sqrt{3}}{3}$h |
17.下列说法不正确的是( )
| A. | 伽利略认为物体的自然状态是静止的,力是维持物体运动的原因 | |
| B. | 亚里士多德认为力是维持物体运动的原因 | |
| C. | 牛顿认为力的真正的效应总是改变物体的速度,即产生加速度 | |
| D. | 伽利略根据理想实验推论出,如果没有摩擦,在水平面上的物体,一旦具有某一个速度,将保持这个速度继续运动下去 |
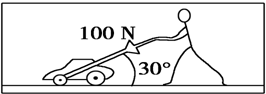 如图所示工人在推一台割草机,其推力F=100N,方向与水平面夹角为30°.
如图所示工人在推一台割草机,其推力F=100N,方向与水平面夹角为30°.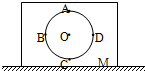 如图所示,在质量为M的物体内,有光滑的圆形轨道,有一质量为m的小球在竖直平面内沿圆轨道做圆周运动,A与C两点分别是轨道的最高点和最低点,B、D两点与圆心O在同一水平面上,在小球运动过程中物体M静止于地面,则小球运动到B点时,物体对地面的压力F=Mg,物体受到摩擦力的方向向右.
如图所示,在质量为M的物体内,有光滑的圆形轨道,有一质量为m的小球在竖直平面内沿圆轨道做圆周运动,A与C两点分别是轨道的最高点和最低点,B、D两点与圆心O在同一水平面上,在小球运动过程中物体M静止于地面,则小球运动到B点时,物体对地面的压力F=Mg,物体受到摩擦力的方向向右.