题目内容
4. 在竖直平面内有一矩形区域ABCD,AB边长L,AD边长2L,F为AD边中点,G为BC边中点,线段FG将ABCD分成两个场区.如图所示,场区Ⅰ内有一竖直向下的匀强电场,场区Ⅱ内有方向大小未知的匀强电场(图中未画出)和方向垂直ABCD平面内的匀强磁场,一个质量为m,电量为+q的带电小球以平行于BC边的速度v从AB边的中点P进入场区Ⅰ,从FG边飞出场区Ⅰ时速度方向改变了37°,小球进入场区Ⅱ做匀速圆周运动,求:
在竖直平面内有一矩形区域ABCD,AB边长L,AD边长2L,F为AD边中点,G为BC边中点,线段FG将ABCD分成两个场区.如图所示,场区Ⅰ内有一竖直向下的匀强电场,场区Ⅱ内有方向大小未知的匀强电场(图中未画出)和方向垂直ABCD平面内的匀强磁场,一个质量为m,电量为+q的带电小球以平行于BC边的速度v从AB边的中点P进入场区Ⅰ,从FG边飞出场区Ⅰ时速度方向改变了37°,小球进入场区Ⅱ做匀速圆周运动,求:(1)场区Ⅱ中的电场强度E2大小及方向;
(2)场区Ⅰ中的电场强度E1的大小;
(3)要使小球能在场区Ⅱ内从FG边重新回到场区Ⅰ的磁感应强度B的最小值.
分析 (1)小球在区域Ⅱ做匀速圆周运动,电场力与重力平衡,洛仑兹力提供向心力,根据平衡条件列式求解;
(2)在区域Ⅰ中,球受重力和向下的电场力,做类似平抛运动,根据分运动公式和牛顿第二定律列式求解;
(3)在区域Ⅱ中,小球做匀速圆周运动,磁感应强度越小,轨道半径越大,临界情况是轨迹与EG相切,画出运动轨迹,结合几何关系得到轨道半径,根据牛顿第二定律列式求解最小磁感应强度大小.
解答 解:(1)在区域Ⅱ做匀速圆周运动,电场力与重力平衡,洛仑兹力提供向心力,故:
qE2=mg
解得:
E2=$\frac{mg}{q}$ 方向竖直向上;
(2)类似平抛运动的时间t=$\frac{L}{v}$,
速度偏转角为37°,故tan37°=$\frac{{v}_{y}}{v}=\frac{at}{v}$,
联立解得:a=$\frac{3{v}^{2}}{4L}$;
根据第二定律,有:qE1+mg=ma,
联立解得:${E_1}=\frac{{\frac{{3m{v^2}}}{4L}-mg}}{q}$
(3)画出小球的运动的临界轨迹,如图所示:
对类平抛运动过程,有:y=$\frac{1}{2}a{t}^{2}=\frac{3}{8}L$,
结合几何关系,有:R+Rcos37°=$\frac{L}{2}+\frac{3}{8}L$,故R=$\frac{35}{72}L$;
场区Ⅱ时小球速度v′=$\frac{5}{4}v$;
根据牛顿第二定律,有:$Bqv′=m\frac{v{′}^{2}}{R}$,
解得:R=$\frac{mv′}{Bq}$,
故B=$\frac{18mv}{7qL}$;
答:(1)场区Ⅱ中的电场强度E2大小为$\frac{mg}{q}$,方向竖直向上;
(2)场区Ⅰ中的电场强度E1的大小为$\frac{\frac{3m{v}^{2}}{4L}-mg}{q}$;
(3)要使小球能在场区Ⅱ内从FG边重新回到场区Ⅰ的磁感应强度B的最小值为$\frac{18mv}{7qL}$.
点评 本题关键是明确小球先做类似平抛运动,后做匀速圆周运动,根据分运动公式和牛顿第二定律列式,同时要画出轨迹进行分析.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 根据《日经新闻》的报道,日本将在2020年东京奥运会开幕之前使“无人驾驶”汽车正式上路并且投入运营.高度详细的3D地图技术能够为“无人驾驶”汽车提供大量可靠的数据,这些数据可以通过汽车内部的机器学习系统进行全面的分析,以执行不同的指令.如图所示为一段公路拐弯处的3D地图,你认为以下说法正确的是( )
根据《日经新闻》的报道,日本将在2020年东京奥运会开幕之前使“无人驾驶”汽车正式上路并且投入运营.高度详细的3D地图技术能够为“无人驾驶”汽车提供大量可靠的数据,这些数据可以通过汽车内部的机器学习系统进行全面的分析,以执行不同的指令.如图所示为一段公路拐弯处的3D地图,你认为以下说法正确的是( )| A. | 如果弯道是水平的,则“无人驾驶”汽车在拐弯时受到重力、支持力、摩擦力和向心力 | |
| B. | 如果弯道是水平的,则“无人驾驶”汽车在拐弯时收到的指令应让车速小一点,防止汽车作离心运动而发生侧翻 | |
| C. | 如果弯道是倾斜的,3D地图上应标出内(东)高外(西)低 | |
| D. | 如果弯道是倾斜的,3D地图上应标出外(西)高内(东)低 |
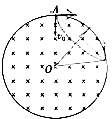 如图所示,在半径为R的圆形区域内有一磁感应强度方向垂直于纸面向里的匀强磁场,一质量为m且带正电的粒子(重力不计)以初速度v0从圆形边界上A点正对圆心射入该磁场区域,若该带电粒子在磁场中运动的轨迹半径为$\sqrt{3}$R,则下列说法中正确的是( )
如图所示,在半径为R的圆形区域内有一磁感应强度方向垂直于纸面向里的匀强磁场,一质量为m且带正电的粒子(重力不计)以初速度v0从圆形边界上A点正对圆心射入该磁场区域,若该带电粒子在磁场中运动的轨迹半径为$\sqrt{3}$R,则下列说法中正确的是( )| A. | 该带电粒子在磁场中将向左偏转 | |
| B. | 该带电粒子在磁场中运动的时间为$\frac{\sqrt{3}πR}{3{v}_{0}}$ | |
| C. | 该带粒子的轨迹圆弧对应的圆心角为30° | |
| D. | 若增大磁场的磁感应强度,则该带电粒子在磁场中运动的轨道半径将变大 |
 如图所示,匀强磁场分布在平面直角坐标系的整个第I象限内,磁感应强度为B、方向垂直于纸面向里.一质量为m、电荷量绝对值为q、不计重力的粒子,以某速度从O点沿着与y轴夹角为30°的方向进入磁场,运动到A点时,粒子速度沿x轴正方向.下列判断正确的是( )
如图所示,匀强磁场分布在平面直角坐标系的整个第I象限内,磁感应强度为B、方向垂直于纸面向里.一质量为m、电荷量绝对值为q、不计重力的粒子,以某速度从O点沿着与y轴夹角为30°的方向进入磁场,运动到A点时,粒子速度沿x轴正方向.下列判断正确的是( )| A. | 粒子带正电 | |
| B. | 粒子由O到A经历的时间t=$\frac{πm}{6qB}$ | |
| C. | 若已知A到x轴的距离为d,则粒子速度大小为$\frac{2qBd}{m}$ | |
| D. | 离开第Ⅰ象限时,粒子的速度方向与x轴正方向的夹角为60° |
 如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上. A、B 间 的动摩擦因数为μ,B与地面间的动摩擦因数为$\frac{1}{2}$μ.最大静摩擦力等于滑动摩擦力,重力加速度为g.现对A施加一水平拉力F,则( )
如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上. A、B 间 的动摩擦因数为μ,B与地面间的动摩擦因数为$\frac{1}{2}$μ.最大静摩擦力等于滑动摩擦力,重力加速度为g.现对A施加一水平拉力F,则( )| A. | 当F<2μmg 时,A、B 都相对地面静止 | |
| B. | 当F=$\frac{5}{2}$μmg时,A的加速度为$\frac{1}{3}$μg | |
| C. | 当F>3 μmg 时,A相对B滑动 | |
| D. | 无论F为何值,B的加速度不会超过$\frac{1}{2}$μg |
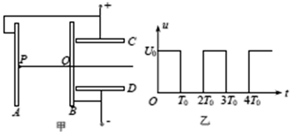 如图甲所示,两组平行正对金属板A、B和C、D,C、D的左端紧靠B板,A与C、B与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生比荷($\frac{q}{m}$)为k的带正电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻紧贴D板的右边缘离开,求:
如图甲所示,两组平行正对金属板A、B和C、D,C、D的左端紧靠B板,A与C、B与D分别连接后,接上如图乙所示规律变化的电压,忽略极板正对部分之外的电场.位于A板中心P处的粒子源可以产生比荷($\frac{q}{m}$)为k的带正电粒子,粒子的重力和初速度均可忽略不计.已知t=0时刻产生的粒子,恰好在t=2T0时刻从B板中心的小孔Q处穿过,并在t=3T0时刻紧贴D板的右边缘离开,求: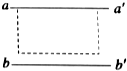 如图所示,某同学在利用插针法测定玻璃砖折射率的实验中误将界面bb′画得离开玻璃砖边缘一段距离,但自己并未察觉.则他测得的折射率将小于(填“大于”、“等于”或“小于”真实值).
如图所示,某同学在利用插针法测定玻璃砖折射率的实验中误将界面bb′画得离开玻璃砖边缘一段距离,但自己并未察觉.则他测得的折射率将小于(填“大于”、“等于”或“小于”真实值). 电了的发现揭开了人类对原子结构的认识.汤姆生用来测定电子的比荷的实验装置如图所示.真空管内的阴极K发出的电子(不计初速度、重力和电子间的相互作用).经加速电压加速后,穿过A′中心的小孔沿中心轴OO′的方向进入到两块水平正对放置的平行极板P和P′间的区域.
电了的发现揭开了人类对原子结构的认识.汤姆生用来测定电子的比荷的实验装置如图所示.真空管内的阴极K发出的电子(不计初速度、重力和电子间的相互作用).经加速电压加速后,穿过A′中心的小孔沿中心轴OO′的方向进入到两块水平正对放置的平行极板P和P′间的区域.