题目内容
2. 如图甲所示,质量m=6kg的空木箱静止在水平面上,某同学用水平恒力F推着木箱向前运动,1s后撤掉推力,木箱运动的v-t图象如图乙所示,不计空气阻力,g取10m/s2.下列说法正确的是( )
如图甲所示,质量m=6kg的空木箱静止在水平面上,某同学用水平恒力F推着木箱向前运动,1s后撤掉推力,木箱运动的v-t图象如图乙所示,不计空气阻力,g取10m/s2.下列说法正确的是( )| A. | 木块与水平面间的动摩擦因数μ=0.25 | |
| B. | 推力F的大小为20N | |
| C. | 在0~3s内,木箱克服摩擦力做功为450J | |
| D. | 在0.5s时,推力F的瞬时功率为450W |
分析 根据速度时间图线得出匀减速直线运动的加速度大小,结合牛顿第二定律求出木块与水平面间的动摩擦因数.根据速度时间图线求出匀加速直线运动的加速度大小,结合牛顿第二定律求出推力的大小.根据速度时间图线围成的面积求出位移的大小,结合摩擦力的大小求出克服摩擦力做功的大小.根据速度时间公式求出0.5s末的瞬时速度,结合P=Fv求出推力F的瞬时功率.
解答 解:A、撤去推力后,木箱做匀减速直线运动,由速度时间图线知,匀减速直线运动的加速度大小${a}_{2}=\frac{10}{2}m/{s}^{2}=5m/{s}^{2}$,根据牛顿第二定律得,${a}_{2}=\frac{μmg}{m}=μg$,解得木块与水平面间的动摩擦因数μ=0.5,故A错误.
B、匀加速直线运动的加速度大小${a}_{1}=\frac{10}{1}m/{s}^{2}=10m/{s}^{2}$,根据牛顿第二定律得,F-μmg=ma1,解得推力F=μmg+ma1=0.5×60+6×10N=90N,故B错误.
C、0-3s内,木箱的位移x=$\frac{1}{2}×3×10m=15m$,则木箱克服摩擦力做功Wf=μmgx=0.5×60×15J=450J,故C正确.
D、0.5s时木箱的速度v=a1t1=10×0.5m/s=5m/s,则推力F的瞬时功率P=Fv=90×5W=450W,故D正确.
故选:CD.
点评 本题考查了牛顿第二定律、运动学公式和功率的基本运用,知道图线的斜率表示加速度,图线围成的面积表示位移.

练习册系列答案
相关题目
12. 如图所示,竖直平面内有一固定光滑半圆形细杆,圆心为O,物体A、B间用轻绳绕过光滑定滑轮彼此连接,B套在细杆上,定滑轮在O点正上方,A置于光滑水平桌面上,初始状态物体A、B位置如图,且均静止.用恒力F拉A,在使小球B拉到P点正下方C点的过程中,( )
如图所示,竖直平面内有一固定光滑半圆形细杆,圆心为O,物体A、B间用轻绳绕过光滑定滑轮彼此连接,B套在细杆上,定滑轮在O点正上方,A置于光滑水平桌面上,初始状态物体A、B位置如图,且均静止.用恒力F拉A,在使小球B拉到P点正下方C点的过程中,( )
 如图所示,竖直平面内有一固定光滑半圆形细杆,圆心为O,物体A、B间用轻绳绕过光滑定滑轮彼此连接,B套在细杆上,定滑轮在O点正上方,A置于光滑水平桌面上,初始状态物体A、B位置如图,且均静止.用恒力F拉A,在使小球B拉到P点正下方C点的过程中,( )
如图所示,竖直平面内有一固定光滑半圆形细杆,圆心为O,物体A、B间用轻绳绕过光滑定滑轮彼此连接,B套在细杆上,定滑轮在O点正上方,A置于光滑水平桌面上,初始状态物体A、B位置如图,且均静止.用恒力F拉A,在使小球B拉到P点正下方C点的过程中,( )| A. | 小球B的机械能不守恒 | |
| B. | 小球B的动能的增加量等于绳子拉力对小球做的功 | |
| C. | 拉力F的功等于A、B两球机械能的增加量 | |
| D. | A的机械能增量为0,B球到C点处时B球的机械能最大 |
13.关于速度和加速度的关系,以下说法正确的是( )
| A. | 物体的速度为零时,其加速度必然为零 | |
| B. | 物体的加速度为零时,其运动速度不一定为零 | |
| C. | 运动物体的速度变化越大,其加速度也越大 | |
| D. | 物体的加速度越小,物体的速度变化也越小 |
10.某质点的v-t图象如图所示,则( )


| A. | 前2s质点做匀加速直线运动 | B. | 4~6 s内质点匀速直线运动 | ||
| C. | 3 s末质点速度是5 m/s | D. | 8 s末质点回到原出发点 |
17.关于位移和路程,下列说法正确的是( )
| A. | 物体沿直线向某一方向运动,通过的路程等于位移的大小 | |
| B. | 物体通过一段路程,其位移不可能为零 | |
| C. | 物体沿直线某一方向运动,通过的路程就是位移 | |
| D. | 物体通过的路程不等,位移也一定不等 |
7.完全相同的两金属小球,相距为d(d远大于小球的直径),分别带有q和3q的电荷量,其相互作用的引力为F,现将两小球接触,然后分开,放回原处,则它们相互作用的库伦力为( )
| A. | $\frac{F}{3}$,引力 | B. | $\frac{F}{3}$,斥力 | C. | $\frac{4F}{3}$,引力 | D. | $\frac{4F}{3}$,斥力 |
11.下列说法正确的是( )
| A. | 给电风扇供电时,电能全部转化为机械能 | |
| B. | 给电风扇供电时,电能主要转化为内能 | |
| C. | 给电热器供电时,电能几乎全部转化为内能 | |
| D. | 给电热器供电时,只有很少一部分电能转化为内能 |
3.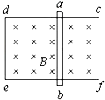 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
 如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,固定于水平面上的金属框cdef处在竖直向下的匀强磁场中,金属棒ab搁在框架上,与ed构成一个边长为l的正方形,金属棒电阻为r,其余电阻不计,开始时磁感应强度为B0,金属棒静止.若以t=0时起,磁感应强度均匀增加,每秒增加量为k,则( )| A. | 金属棒中的感应电流的方向为b→a | |
| B. | 金属棒中的感应电流的大小为$\frac{{k{l^{\;}}}}{r}$ | |
| C. | 金属棒消耗的电功率为$\frac{{k}^{2}{l}^{4}}{r}$ | |
| D. | 若t=t1时金属棒仍然静止,金属棒受到的最大静摩擦力不能小于(B0+kt1)$\frac{{k{l^3}}}{r}$ |
 用螺旋测微器测量一根合金丝的直径,为防止读数时测微螺杆发生转动,读数前应先旋紧图示的部件C(选填“A”、“B”、“C”或“D”),从图中的示数可读出合金丝的直径为0.410mm.
用螺旋测微器测量一根合金丝的直径,为防止读数时测微螺杆发生转动,读数前应先旋紧图示的部件C(选填“A”、“B”、“C”或“D”),从图中的示数可读出合金丝的直径为0.410mm.