题目内容
10.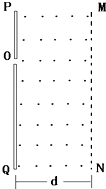 如图所示,竖直放置的足够长的绝缘板PQ右方的区域内有垂直纸面向外的匀强磁场,磁感应强度的大小B=5.0×10-2T,MN是与PQ平行的磁场的右边界,d=0.2m,在PQ上的小孔O处有一放射源,放射源沿纸面向磁场中各个方向均匀的射出速率v=2×106m/s的某种带正电的粒子,粒子的质量m=1.6×10-27kg,所带电荷量q=3.2×10-19C,不计粒子的重力及粒子间的相互作用.
如图所示,竖直放置的足够长的绝缘板PQ右方的区域内有垂直纸面向外的匀强磁场,磁感应强度的大小B=5.0×10-2T,MN是与PQ平行的磁场的右边界,d=0.2m,在PQ上的小孔O处有一放射源,放射源沿纸面向磁场中各个方向均匀的射出速率v=2×106m/s的某种带正电的粒子,粒子的质量m=1.6×10-27kg,所带电荷量q=3.2×10-19C,不计粒子的重力及粒子间的相互作用.(1)求带电粒子在磁场中的轨迹半径;
(2)求粒子的周期和从边界MN射出的粒子在磁场中运动的最短时间;
(3)若OQ=$\frac{\sqrt{3}}{5}$m,且QN是磁场的下边界,则在某段时间内从放射源共射出n个粒子中,有多少个粒子是从磁场的下边界QN射出的?
分析 (1)带电粒子在磁场中做匀速圆周运动,由洛伦兹力充当向心力,由牛顿第二定律求解轨迹半径.
(2)因为粒子运动的轨道半径相同,故弦最短时对应的圆心角最小,运动时间最短,根据几何关系得到最短的弦的大小,再求解最短时间.
(3)画出粒子恰好能从磁场的下边界射出的运动轨迹,由数学知识得到圆心角,再求解即可.
解答 解:(1)由qvB=m$\frac{{v}^{2}}{r}$
得r=$\frac{mv}{qB}$=$\frac{1.6×1{0}^{-27}×2×1{0}^{6}}{3.2×1{0}^{-19}×5×1{0}^{-2}}$m=0.2m
(2)因为粒子运动的轨道半径相同,故弦最短时对应的圆心角最小,运动时间最短,显然最短的弦的大小为d,易得此时的圆心角θ=$\frac{π}{3}$
粒子做圆周运动的周期T=$\frac{2πr}{v}$=$\frac{2πm}{qB}$
最短时间t=$\frac{θ}{2π}$T=$\frac{T}{6}$=$\frac{π}{3}$×10-7s
(3)如图中1轨迹所示,当速度与0P的夹角θ=90°时,恰好能从磁场的下边界射出
当粒子恰好从Q点射出时,如图中2轨迹所示设此时的圆心角为α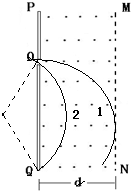
则sin$\frac{α}{2}$=$\frac{\frac{OQ}{2}}{r}$=$\frac{\sqrt{3}}{2}$
此时粒子从O点射出时的速度方向与OP的夹角为α=120°,故θ=120°
△θ=120°-90°=30°
故从磁场的下边界QN射出的粒子数为$\frac{30°}{180°}$n=$\frac{n}{6}$
答:
(1)带电粒子在磁场中的轨迹半径为0.2m;
(2)粒子的周期和从边界MN射出的粒子在磁场中运动的最短时间是$\frac{π}{3}$×10-7s;
(3)若OQ=$\frac{\sqrt{3}}{5}$m,且QN是磁场的下边界,则在某段时间内从放射源共射出n个粒子中,有$\frac{n}{6}$个粒子是从磁场的下边界QN射出的.
点评 本题中带电粒子在匀强磁场中运动的类型,画出粒子的运动轨迹,运用几何知识和牛顿第二定律研究磁场中轨迹问题.

| A. | 两物体下落过程中,在同一时刻甲的速度比乙的速度大 | |
| B. | 各自下落1m时,它们的速度相同 | |
| C. | 下落过程中甲的加速度比乙的加速度大 | |
| D. | 甲乙经过同一高度处,它们的速度相同 |
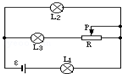 如图所示的电路,L1、L2和L3为三个相同的灯泡,灯泡电阻大于电源内阻,当变阻器R的滑片P向左移动时,下列说法中不正确的是( )
如图所示的电路,L1、L2和L3为三个相同的灯泡,灯泡电阻大于电源内阻,当变阻器R的滑片P向左移动时,下列说法中不正确的是( )| A. | L1、L3两灯变亮,L2灯变暗 | |
| B. | L2灯中电流变化值小于L3灯中电流变化值 | |
| C. | 电源输出功率增大 | |
| D. | 电源的供电效率增大 |
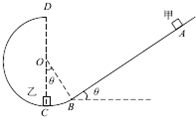 如图所示,光滑的圆弧轨道与倾角为θ=37°的斜面相切于B点,在圆弧轨道的最低点C放一质量为m的物块乙,圆弧轨道的半径为R,质量为2m的物块甲在斜面上A点由静止释放,物块甲与斜面的动摩擦因数为μ=$\frac{1}{6}$,AB间距离为3R,甲、乙碰撞后,乙恰好能到达圆弧轨道的最高点D点,(已知sin37°=0.6,cos37°=0.8)求:
如图所示,光滑的圆弧轨道与倾角为θ=37°的斜面相切于B点,在圆弧轨道的最低点C放一质量为m的物块乙,圆弧轨道的半径为R,质量为2m的物块甲在斜面上A点由静止释放,物块甲与斜面的动摩擦因数为μ=$\frac{1}{6}$,AB间距离为3R,甲、乙碰撞后,乙恰好能到达圆弧轨道的最高点D点,(已知sin37°=0.6,cos37°=0.8)求: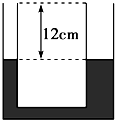 如图所示,两端开口的U形玻璃管两边粗细不同,粗管横截面积是细管的2倍.管中装入水银,两管中水银面与管口距离均为12cm,大气压强为p0=75cmHg.现将粗管管口封闭,然后将细管管口用一活塞封闭并使活塞缓慢推入管中,直至两管中水银面高度差达6cm为止.求:
如图所示,两端开口的U形玻璃管两边粗细不同,粗管横截面积是细管的2倍.管中装入水银,两管中水银面与管口距离均为12cm,大气压强为p0=75cmHg.现将粗管管口封闭,然后将细管管口用一活塞封闭并使活塞缓慢推入管中,直至两管中水银面高度差达6cm为止.求: 在某次“20米折返跑”测试中,受试者在平直跑道上听到“跑”的口令后,在起点终点线前全力跑向正前方20米处的折返线,测试员同时开始计时.受试者到达折返线时,用手触摸折返线处的物体(如木箱),再转身跑向起点终点线,当胸部到达起点终点线的垂直面时,测试员停表,所计时间即为“折返跑”的成绩,如图所示.设受试者起跑的加速度为4.0m/s2,运动过程中的最大速度为6.4m/s,到达折返线处时需减速到零,加速度的大小为8.0m/s2,返回时达到最大速度后不需减速,保持最大速度冲线.受试者在加速和减速阶段的运动均可视为匀变速直线运动.求该受试者“折返跑”的成绩为多少秒?
在某次“20米折返跑”测试中,受试者在平直跑道上听到“跑”的口令后,在起点终点线前全力跑向正前方20米处的折返线,测试员同时开始计时.受试者到达折返线时,用手触摸折返线处的物体(如木箱),再转身跑向起点终点线,当胸部到达起点终点线的垂直面时,测试员停表,所计时间即为“折返跑”的成绩,如图所示.设受试者起跑的加速度为4.0m/s2,运动过程中的最大速度为6.4m/s,到达折返线处时需减速到零,加速度的大小为8.0m/s2,返回时达到最大速度后不需减速,保持最大速度冲线.受试者在加速和减速阶段的运动均可视为匀变速直线运动.求该受试者“折返跑”的成绩为多少秒?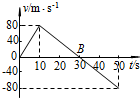 飞船在火箭作用下从某一星球表面竖直升空,假设火箭对飞船的推动力为恒力,火箭上升到一定高度后,与飞船分离,飞船在星球引力作用下运动.如图是飞船沿竖直方向的速度随时间变化的情况.已知飞船的质量为500kg.求
飞船在火箭作用下从某一星球表面竖直升空,假设火箭对飞船的推动力为恒力,火箭上升到一定高度后,与飞船分离,飞船在星球引力作用下运动.如图是飞船沿竖直方向的速度随时间变化的情况.已知飞船的质量为500kg.求 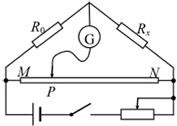 用图所示的电路可以测量电阻的阻值.Rx是待测电阻,定值电阻R0=10Ω,G是灵敏度很高的电流表,MN是一段均匀的电阻丝.闭合开关,改变滑动头P的位置,当通过电流表 G的电流为零时,测得MP=2cm,PN=7cm,则Rx的阻值为35Ω.
用图所示的电路可以测量电阻的阻值.Rx是待测电阻,定值电阻R0=10Ω,G是灵敏度很高的电流表,MN是一段均匀的电阻丝.闭合开关,改变滑动头P的位置,当通过电流表 G的电流为零时,测得MP=2cm,PN=7cm,则Rx的阻值为35Ω.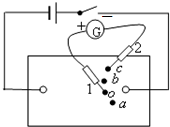 如图所示,为描绘电场中等势线的装置,若所用电流计的电流从哪一接线柱流入,其指针就向哪一侧偏,在寻找基准点O的另一等势点时,探针1与O点接触,探针2与导电纸上的C点接触电流计的指针向负接线柱一侧偏转,为了尽快找到新等势点,探针2应由C点逐渐向左移动(填“右”或者“左”).
如图所示,为描绘电场中等势线的装置,若所用电流计的电流从哪一接线柱流入,其指针就向哪一侧偏,在寻找基准点O的另一等势点时,探针1与O点接触,探针2与导电纸上的C点接触电流计的指针向负接线柱一侧偏转,为了尽快找到新等势点,探针2应由C点逐渐向左移动(填“右”或者“左”).