题目内容
12.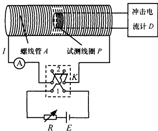 如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度Dφ=$\frac{{d}_{m}}{N△Φ}$,式中△为单匝试测线圈磁通量的变化量.则试测线圈所在处磁感应强度大小B=$\frac{{d}_{m}}{2N{D}_{∅}S}$;若将K从位置1拨到位置2的过程所用的时间为△t,则试测线圈P中产生的平均感应电动势$\overline{E}$=$\frac{{d}_{m}}{{D}_{∅}△t}$.
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度Dφ=$\frac{{d}_{m}}{N△Φ}$,式中△为单匝试测线圈磁通量的变化量.则试测线圈所在处磁感应强度大小B=$\frac{{d}_{m}}{2N{D}_{∅}S}$;若将K从位置1拨到位置2的过程所用的时间为△t,则试测线圈P中产生的平均感应电动势$\overline{E}$=$\frac{{d}_{m}}{{D}_{∅}△t}$.
分析 开关K从位置1拨到位置2时,所形成的磁场方向发生改变,注意根据磁通量的定义式和法拉第电磁感应定律求解即可.
解答 解:设试测线圈所在处磁感应强度大小为B,则K从位置1拨到位置2磁通量的变化量大小为:△Φ=2Bs
结合Dφ=$\frac{{d}_{m}}{N△Φ}$解得:B=$\frac{{d}_{m}}{2N{D}_{∅}S}$;
线圈中电动势为:E=n$\frac{△∅}{△t}$
所以解得:E=$\frac{{d}_{m}}{{D}_{∅}△t}$.
故答案为:$\frac{{d}_{m}}{2N{D}_{∅}S}$,$\frac{{d}_{m}}{{D}_{∅}△t}$.
点评 本题考查巧妙,新颖,通过实验考查了对法拉第电磁感应的理解和应用,在平时训练中要通过各种角度、途径来理解基本规律.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
3.下列说法正确的是( )
| A. | 变速运动一定是曲线运动 | |
| B. | 物体受恒力作用不可能做曲线运动 | |
| C. | 平抛运动是变加速运动 | |
| D. | 做平抛运动的物体速度变化的方向始终是竖直向下的 |
20. 如图所示,不计分别为R、2R的两个水平圆盘,小圆盘转动时会带动大圆盘不打滑的一起转动.质量为m的小物块甲放置在打圆盘上距离转轴R处,质量为2m的小物块放置在小圆盘的边缘处.它们与盘面间的动摩擦因数相同,当小圆盘以角速度ω转动时,两物块均相对圆盘静止,下列说法正确的是( )
如图所示,不计分别为R、2R的两个水平圆盘,小圆盘转动时会带动大圆盘不打滑的一起转动.质量为m的小物块甲放置在打圆盘上距离转轴R处,质量为2m的小物块放置在小圆盘的边缘处.它们与盘面间的动摩擦因数相同,当小圆盘以角速度ω转动时,两物块均相对圆盘静止,下列说法正确的是( )
 如图所示,不计分别为R、2R的两个水平圆盘,小圆盘转动时会带动大圆盘不打滑的一起转动.质量为m的小物块甲放置在打圆盘上距离转轴R处,质量为2m的小物块放置在小圆盘的边缘处.它们与盘面间的动摩擦因数相同,当小圆盘以角速度ω转动时,两物块均相对圆盘静止,下列说法正确的是( )
如图所示,不计分别为R、2R的两个水平圆盘,小圆盘转动时会带动大圆盘不打滑的一起转动.质量为m的小物块甲放置在打圆盘上距离转轴R处,质量为2m的小物块放置在小圆盘的边缘处.它们与盘面间的动摩擦因数相同,当小圆盘以角速度ω转动时,两物块均相对圆盘静止,下列说法正确的是( )| A. | 小物块甲受到的摩擦力大小为$\frac{1}{4}$mω2R | |
| B. | 两物块的线速度大小相等 | |
| C. | 在角速度ω逐渐增大的过程中,物块甲先滑动 | |
| D. | 在角速度ω逐渐减小的过程中,摩擦力对两物块做负功 |
4.物体沿直线运动,下列说法中正确的是( )
| A. | 若物体某1秒内的平均速度是5m/s则物体在这1s内的位移一定是5m | |
| B. | 若物体在第1s末的速度是5m/s,则物体在第1s内的位移一定是5m | |
| C. | 若物体在10s内的平均速度是5m/s,则物体在其中1s内的位移一定是5m | |
| D. | 物体通过10m的位移平均速度是5m/s,则物体在通过这段位移的时间一定是2s |
1. 如图所示,质量为m=2kg的小球,以v0=15m/s的初速度,朝着一个倾角为θ=37°的斜面平抛出去,它落到斜面上时的速度方向刚好和斜面垂直,则( )
如图所示,质量为m=2kg的小球,以v0=15m/s的初速度,朝着一个倾角为θ=37°的斜面平抛出去,它落到斜面上时的速度方向刚好和斜面垂直,则( )
 如图所示,质量为m=2kg的小球,以v0=15m/s的初速度,朝着一个倾角为θ=37°的斜面平抛出去,它落到斜面上时的速度方向刚好和斜面垂直,则( )
如图所示,质量为m=2kg的小球,以v0=15m/s的初速度,朝着一个倾角为θ=37°的斜面平抛出去,它落到斜面上时的速度方向刚好和斜面垂直,则( )| A. | 该小球落到斜面上的瞬间重力对小球做功的即时功率为400W | |
| B. | 该小球落到斜面上的瞬间重力对小球做功的即时功率为200W | |
| C. | 整个平抛运动过程中重力对小球做功的平均功率为400W | |
| D. | 整个平抛运动过程中重力对小球做功的平均功率为200W |
2.关于曲线运动,以下说法中正确的是( )
| A. | 做曲线运动的物体,受到的合力可能为零 | |
| B. | 做曲线运动的物体,加速度一定是变化的 | |
| C. | 做曲线运动的物体,速度的方向一定是变化的 | |
| D. | 做曲线运动的物体,速度的大小一定是变化的 |
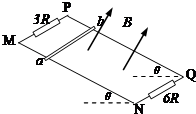 如图,MN、PQ两条平行的光滑金属轨道与水平面成θ角固定,轨距为d.空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B.P、M间接有阻值为3R的电阻.Q、N间接有阻值为6R的电阻,质量为m的金属杆ab水平放置在轨道上,其有效电阻为R.现从静止释放ab,当它沿轨道下滑距离s时,达到最大速度.若轨道足够长且电阻不计,重力加速度为g.求:
如图,MN、PQ两条平行的光滑金属轨道与水平面成θ角固定,轨距为d.空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B.P、M间接有阻值为3R的电阻.Q、N间接有阻值为6R的电阻,质量为m的金属杆ab水平放置在轨道上,其有效电阻为R.现从静止释放ab,当它沿轨道下滑距离s时,达到最大速度.若轨道足够长且电阻不计,重力加速度为g.求: