题目内容
9．
如图所示，在氢原子能级图中，氢原子从各个较高能级跃迁至同一较低能级时，会发出一系列光谱线，形成谱线系，分别称为赖曼线系，巴耳末线系，帕邢线系等．在同一谱线系中，下列说法正确的是（ ）| A． | 每一跃迁都会释放出一个电子，使原子变为粒子 | |
| B． | 各种跃迁都会释放出不同能量的光子 | |
| C． | 各条谱线具有相同的频率 | |
| D． | 跃迁后原子的能级是相同的 |
分析 能级间跃迁辐射或吸收的光子能量必须等于两能级间的能级差，能级差越大，辐射的光子能量越大，频率越大，波长越小．
解答 解：A、氢原子从各个较高能级跃迁至同一较低能级时辐射光子，故A错误；
B、能级间跃迁辐射或吸收的光子能量必须等于两能级间的能级差，各种跃迁能级差不等，所以各种跃迁都释放出不同能量的光子．故B正确；
C、根据光子的吸收和放出满足hγ=Em-En．所以各条光谱线具有不同的频率，故C错误；
D、跃迁后原子的能级是相同的，故D正确；
故选：BD．
点评 解决本题的关键掌握一群氢原子处于激发态能放出光子种数的方法，以及知道光子的吸收和放出满足hγ=Em-En．
练习册系列答案
相关题目
20．
如图所示为原子核的核子平均质量m与核子数的关系图象，其中核子数为56的Fe原子的核子平均质量最小，请结合图象判断：下列说法正确的是（ ）
如图所示为原子核的核子平均质量m与核子数的关系图象，其中核子数为56的Fe原子的核子平均质量最小，请结合图象判断：下列说法正确的是（ ）| A． | A核分裂成B核和C核，释放能量 | B． | E核和F核结合成D核，吸收能量 | ||
| C． | A核的比结合能大于B核的比结合能 | D． | Fe是比结合能最大的元素 |
4．
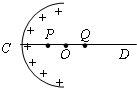已知均为带电球壳内部的电场强度处处为零．将球壳一分为二，取其一半如图所示，所带电荷仍均匀分布在半球面上．CD为通过半球顶点C与球心O的直线，半球壳关于CD对称．P、Q为CD上在O点两侧与O点距离相等的两点．则下列判断正确的是（ ）
已知均为带电球壳内部的电场强度处处为零．将球壳一分为二，取其一半如图所示，所带电荷仍均匀分布在半球面上．CD为通过半球顶点C与球心O的直线，半球壳关于CD对称．P、Q为CD上在O点两侧与O点距离相等的两点．则下列判断正确的是（ ）| A． | P点电场强度大于Q点电场强度 | |
| B． | P点电势高于Q点电势 | |
| C． | 将与带正电微粒沿直线从P点移到到Q点，电场力先做正功后做负功 | |
| D． | 将与带负电微粒从Q点由静止释放，仅在电场力作用下，微粒向P做匀加速运动 |
14．某同学设计了一个“探究加速度a与物体所受合力F及质量m的关系”实验．如图1所示为实验装置简图，A为小车，B为电火花计时器（其接50Hz的交流电），C为装有砝码的 小盘，D为一端带有定滑轮的长方形木板，实验中认为细绳对小车的拉力F等于砝码和小盘的总重力，小车运动的加速度a可用纸带上的打点求得．
（1）电火花计时器应接交流220v电压．
（2）实验中认为细绳对小车的拉力F等于砝码和小盘的总重力，应满足砝码和小盘的总质量远小于小车的质量．
（3）如图2为某次实验得到的纸带，根据纸带可求出小车的加速度大小为3.2 m/s2．（结果保留两位有效数字）
（4）在“探究加速度与质量的关系”时，保持砝码和小盘质量不变，改变小车质量m，分别得到小车加速度a与质量m的数据如下表：
根据上表数据，为直观反映F不变时a与m的关系，请在图3中的方格坐标纸中选择恰当物理量建立坐标系，并作出图线．（如有需要，可利用上表中的空格数据）
（5）在“探究加速度与力的关系”时，保持小车的质量不变，改变小盘中砝码的质量，该同学根据实验数据作出了加速度a与合力F的关系图线如图4所示，该图线不通过坐标原点，试分析图线不通过坐标原点的原因．
答：未平衡摩擦力或平衡摩擦力不足．
（1）电火花计时器应接交流220v电压．
（2）实验中认为细绳对小车的拉力F等于砝码和小盘的总重力，应满足砝码和小盘的总质量远小于小车的质量．
（3）如图2为某次实验得到的纸带，根据纸带可求出小车的加速度大小为3.2 m/s2．（结果保留两位有效数字）
（4）在“探究加速度与质量的关系”时，保持砝码和小盘质量不变，改变小车质量m，分别得到小车加速度a与质量m的数据如下表：
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 小车加速度 a/（m•s-2） | 1.98 | 1.72 | 1.48 | 1.25 | 1.00 | 0.75 | 0.48 | 0.50 | 0.30 |
| 小车质量 m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 0.75 | 1.00 | 1.67 |
（5）在“探究加速度与力的关系”时，保持小车的质量不变，改变小盘中砝码的质量，该同学根据实验数据作出了加速度a与合力F的关系图线如图4所示，该图线不通过坐标原点，试分析图线不通过坐标原点的原因．
答：未平衡摩擦力或平衡摩擦力不足．
19．“嫦娥三号”在月球表面释放出“玉兔”号月球车开展探测工作，若该月球车质量为m，已知地球半径为R1，月球半径为R2，地球和月球表面处的重力加速度分别为g和g月，下列说法正确是（ ）
| A． | 若在月球表面用弹簧秤称该月球车，示数为零 | |
| B． | 若在月球表面用弹簧秤称该月球车，示数为mg月 | |
| C． | 地球与月球的质量之比为$\frac{g{{R}_{1}}^{2}}{{g}_{月}{{R}_{2}}^{2}}$ | |
| D． | 卫星在很靠近地球和月球表面的轨道上做匀速圆周运动的周期之比为$\sqrt{\frac{g{{R}_{1}}^{3}}{{g}_{月}{{R}_{2}}^{3}}}$ |